Modelo de Oferta y Demanda en Matlab

Syms es una función que se utiliza para declarar símbolos o variables simbólicas. Estos símbolos no tienen un valor numérico asignado de forma predeterminada, en contraste con las variables normales en MATLAB que almacenan valores numéricos. En su lugar, los símbolos se utilizan para realizar cálculos simbólicos, como álgebra simbólica, cálculo, manipulación de expresiones matemáticas y resolución de ecuaciones simbólicas.

syms x
ezplot(x^2 - x*1.5, [-2 2])

Puedes utilizar syms en MATLAB para simular las curvas de oferta y demanda mediante ecuaciones simbólicas y luego graficar los resultados. Definiendo con syms las variables del modelo, posteriormente necesitamos definir las expresiones que definen las curvas de oferta y demanda y resolver el sistema de ecuaciones (solve). Posteriormente se utiliza la función subs, que permite remplazar valores dentro de una expresión simbólica. Es decir, dentro de la función demanda, podemos recuperar los valores para el precio de demanda que corresponden a cada una de las cantidades demandadas[1].

 syms P Q
 
oferta = 1.2*Q + 5;
demanda = 10 - 0.45*Q;
 
equilibrio = solve(oferta == demanda, [P, Q]);
 
Q_values = linspace(0, 10, 100); % Valores de Q para el gráfico
 
oferta_values = subs(oferta, Q, Q_values);
demanda_values = subs(demanda, Q, Q_values);

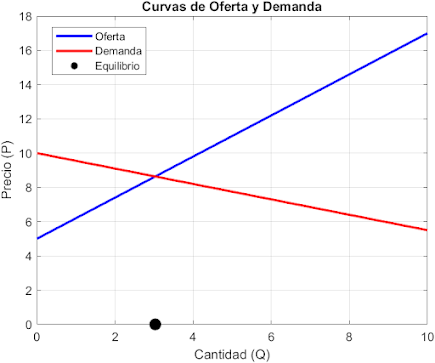
Finalmente, se grafican los resultados. Teniendo en cuenta que, en MATLAB, se utiliza el comando figure antes de crear un gráfico para crear una nueva ventana de figura o lienzo de dibujo en la que se mostrará el gráfico. Esto es útil cuando deseas tener múltiples gráficos en ventanas separadas o cuando deseas personalizar aspectos específicos de la figura, como su tamaño o propiedades. Hold on permite anexar series a un mismo gráfico, como múltiples layers en el caso de ggplot2 para los usuarios de R. Finalmente, se agregan las etiquetas y las opciones sobre formato del gráfico.

figure;
plot(Q_values, oferta_values, 'b', 'LineWidth', 2);
hold on;
plot(Q_values, demanda_values, 'r', 'LineWidth', 2);
scatter(equilibrio.Q, equilibrio.P, 100, 'k', 'filled'); % Punto de equilibrio
xlabel('Cantidad (Q)');
ylabel('Precio (P)');
title('Curvas de Oferta y Demanda');
legend('Oferta', 'Demanda', 'Equilibrio', 'Location','best');
grid on;

[1] syms x y
 
expr = x^2 + y;
valor_x = 3;
valor_y = 4;
 
resultado = subs(expr, [x, y], [valor_x, valor_y]);

4 Curso de Econometría Aplicada en R

Parte I. Introducción a la Economettría

Curso 1. Regresión y naturaleza del análisis econométrico

Clase 1. Naturaleza del modelo Econometríco

Clase 2. Repaso de inferencia estadística

Clase 3. Modelo de regresión

Clase 4. Modelo de regresión múltiple

Clase 5. Modelo de regresión en R

Curso 2. Análisis del modelo de regresión y econometría aplicada

Clase 6. Test de hipótesis 

Clase 7. Inferencia sobre el modelo de regresión en R

Clase 8. Formas funcionales y variables discretas

Clase 9. Formas funcionales en R

Clase 10. Selección de modelos en R

Parte II. Microeconometría y datos de Panel

Curso 3. Microeconometría y datos de panal

Clase 1. Causalidad estadística

Clase 2. Endogeneidad y variables instrumentales

Clase 3. Modelos de probabilidad

Clase 4. Panel estatico 

Parte III. Econometría Financiera y de Series Temporales

Curso 4. Econometría financiera en R

Clase 1. Modelos ARIMA en R

Clase 2. Modelos de volatilidad (GARCH en R)

Clase 3. Modelos factoriales y riesgo sistémico 

Clase 4. Valor en riesgo (VaR)

Clase 5. Vectores autoregresivos (VAR)

Métodos cuantitativos y herramientas para el análisis empírico de las condiciones de Competencia

La siguiente entrada constituye una recopilación de notas sobre metodologías y herramientas utilizadas para el estudio de la competencia. Presenta los apuntes realizados durante mi experiencia trabajando en el Departamento de Estudios Económicos y de Mercado de la Comisión Nacional de Defensa de la Competencia y pretende servir como elementos de referencia rápida al momento de abordar el estudio de la competencia de algún sector, presentando las principales metodologías y recomendando lecturas básicas y aplicadas, que permiten la introducción al conocimiento del tema.

Clase 0. Economía Industrial y Políticas de Competencia en República Dominicana

Clase 1. Preliminares microeconómicos y econométricos

Clase 2. Métodos cuantitativos para la determinación del mercado relevante
      2.1. Análisis de sustituibilidad
      2.1.1. Modelos de demanda y elasticidades
      2.1.2. Test del monopolista hipotético
      2.2. Test de precios: correlación, causalidad, cointegración
      2.3. Mercado geográfico
      2.3.1. flujos comerciales
      2.3.2. Análisis de cointegración
      2.4. Test de perdida critica

Clase 3. Estrucutra del mercado e indicadores de concentración

Clase 4. Barreras de entrada

Clase 5. Técnicas para detectar carteles (screening)
       5.1.Técnicas de detección de carteles
       5.2.Estimación del daño del cartel

       5.2.1. Cartel dating

       5.2.2. Regresión dinámica

Clase 6. Posición de dominio y restricciones verticales

       6.1.Posición dominante
       6.2.Prácticas abusivas
       6.3.Restriccionse verticales
     

Clase 7. Estimación del daño
       7.1. Metodologías para la estimación y tipos de daño
       7.1.1. Analisis estadísticos-econométricos
       7.1.2. Ex-post: comparar productos,  comparar mercados
       7.1.3. Análisis de regresión
       7.1.4. Diferencia en diferencia
       7.2. Análisis de simulaciones
       7.3. Comparar estados e resultados
       7.4. Daño al consumidor

Clase 8. La Evidencia Económica como Elemento de Prueba

       8.1. Peculiaridades de la investigación económica y el estudio de la competencia

       8.2. Reglas per se y el estándar de prueba

       8.3. El uso del análisis económicos en los casos de competencia

Clase 11. Elaboración de un observatorio de competencia (Pro-Competencia)

Sitio en construcción

Estimar un modelo de Oferta y Demanda en Stata

Mediante la ejecución de un modelo de ecuaciones simultaneas se puede reproducir el famoso modelo de oferta y demanda. Usando Stata, el mismo se obtine:

*---------------------------------------
. global demand "(qdeman: qdem precio)"
. global oferta "(qoferta: qofer precio)"
. reg3 $demand $oferta, endog(precio)

El gráfico de oferta y demanda se puede obtener usando el siguiente comando:

*---------------------------------------
. predict demand, equation(qdeman)
. predict oferta, equation(qoferta)

. graph twoay line demand precio, sort || line oferta price

Optimización estática, notas de clases

Resumen del proceso de optimización en problemas libres y restringidos de una, dos y mas variables.

1.       Optimización Libre. La función objetivo no está sujeta a ninguna restricción 

Tipo de Optimización	No. De variables en la función objetivo (Z)	Condición necesaria de primer orden	Condición suficiente de segundo orden
Optimización Libre Optimización Libre	n=1 z = f ( x)	1. Identificar los puntos críticos f’(z) = dy/dx = 0	2. Tomar la segunda derivada, evaluar los puntos críticos, y revisar los signos. f′′(a) < 0, la función es cóncava en “a”, por ende un máximo relativo f′′(a) > 0, la función es convexa en “a”, por ende un mínimo relativo f′′(a) = 0, el test es inconcluso y es necesario realizar el test de las “derivadas sucesivas”
	n=2 z = f ( x1, x2)	1. Las derivadas parciales de primer orden deben simultáneamente ser iguales a cero.	2. Las derivadas parciales de segundo orden deben ser negativas cuando ellas son evaluadas en el punto crítico (a,b) para un máximo relativo y positivas para un mínimo relativo. Máximo: fxx , fyy < 0 y fxx , fyy > (fxy)2 Mínimo: fxx , fyy > 0 y fxx , fyy < (fxy)2
	n>2 z = f ( x1, x2, x3 )	dz es ahora dz = f1dx1 + f2dx2 + f3dx3 Como estos no son nulos, f1 = f2 = f3 = 0 Es decir, el vector gradientes de primeras derivadas deben igualarse a cero.	Estas condiciones se obtienen del determinante de la matriz Hessiana (simétrica por el teorema de Young). Máximo: ∣H1∣ < 0; ∣H2∣ > 0; ∣H3∣ < 0 Mínimo: ∣H1∣, ∣H2∣,..,∣Hn∣>0  Los determinantes hessiano se obtienen de la matriz de segundas derivadas H1, H2… Hn representan los menores principales de la matriz hessiana

1.       2. Optimización restringida

En optimización restringida, las variables están sujetas a cumplir diferentes condiciones. Aquí se distinguen aquellas restricciones de igualdad y de desigualdad. En este tipo de problemas de optimización se quiere determinar los valores de ciertas variables de decisión” que sujetos a las limitaciones de los recursos, optimizan (maximizan o minimizan, dependiendo del problema) una función (García Donato, 2013). La estructura se resume en:

F(x) es la función objetivo, las restricciones forman el conjunto S o conjunto factible, las variables x = (x1, x2, . . . , xn) representan las variables del problema. Ahora la solución a los problemas consisten en encontrar los problemas que optimizan (P) cumpliendo con las restricciones.

1.1. Restricciones de igualdad

Tipo de Optimización	No. De variables en la función objetivo (Z)	Condición necesaria de primer orden	Condición suficiente de segundo orden
Optimización restringida Restricciones de igualdad	n=2 Max. f (x1, x2) S.a. g(x1, x2) = k	1. Se establece la función lagrangeana.[1] F(x1, x2, λ) = f(x1, x2) + λ[ k - g(x1, x2)] Con la restricción es igual a cero, esto no altera la función objetivo Los valores críticos se obtienen igualando a cero el vector gradiente. F1(x1, x2, λ) = 0[2] F2(x1, x2, λ) = 0 F λ (x1, x2, λ) = 0	2.  Para determinar si los valores críticos corresponden a máximos o mínimos, es necesario utilizar el criterio del Hessiano Orlado. noté que las g representan la primeras derivadas de las restricciones  Máximo: Mínimo:

---

[1] Nótese que la función de Lagrange estandariza el proceso de convertir el problema restringido a un problema libre.

[2] F1 representa la derivada parcial de la Lagrangiana respecto a su primera variable independiente (x1)

Nota. El λ que comúnmente se llama multiplicador de lagrange, representa (cambiado de signo) la tasa marginal de variación de la función objetico ante una variación del término independiente de la i-esima restricciones.

1.1. Restricciones de desigualdad (Condiciones de Kunh-Tucker)

Hasta ahora las condiciones matemáticas establecían las condiciones a cumplir por cualquier punto (llamado regulares)[1] para considerarse optimo, sin embargo ahora existen algunos puntos especiales (no regulares) que no están sujetos a cumplir las condiciones necesarias.

Tipo de Optimización	No. De variables en la función objetivo (Z)	Condiciones suficientes y necesarias de primer orden CONDICIONES DE KUNH-TUCKER
Optimización restringida Restricciones de desigualdad	n=2 Max. f (x1, x2) S.a. g(x1, x2) >= k  X1,x2 >=0[1]	para cada una de las restricciones que no son de signo: la siguiente tabla para cada una de las componentes de las   x = (x1, x2, . . . , xn) del problema

Fuente: Tomado de Donato 2013

---

[1] En este problema algunas variables pueden estar sujetas a restricciones de signo. Las variables no sujetas a restricciones de signo las llamaremos libres.

---

[1] Ver página 25 de apuntes de matemáticas, para la clasificación de puntos regulares.