La siguiente entrada utiliza la inflación mensual de la República Dominicana para obtener una descomposición histórica de la evolución de la inflación trimestral en un componente transitorio vs. componente subyacente. Primero se activan las librearas requeridas y se importa la data (dataset), que incluye la fecha mensual y el IPC con datos usando como base la canasta 2019-2020.
# Load the data
setwd(dirname(rstudioapi::getActiveDocumentContext()$path))
library(forecast)
library(lubridate)
library(tidyverse)
fecha ipc
<dttm> <dbl>
2
1984-02-01 00:00:00 1.42
3
1984-03-01 00:00:00 1.44
4
1984-04-01 00:00:00 1.46
5
1984-05-01 00:00:00 1.48
6
1984-06-01 00:00:00 1.54
7
1984-07-01 00:00:00 1.56
8
1984-08-01 00:00:00 1.57
9
1984-09-01 00:00:00 1.64
10 1984-10-01 00:00:00 1.68
# ... with 462 more rows
Posteriormente, se agrega la serie trimestralmente usando el promedio del IPC. Se identifica el trimestre de cada mes (quarter), posteriormente se crea un agregado del promedio trimestral del IPC, y sobre este IPC trimestral, calculamos la inflación trimestral (q_inf). En una entrada anterior se explicó en detalle la agregación temporal y las transformaciones de series temporales.
q_dataset <- dataset |>
mutate(quarter = zoo::as.yearqtr(fecha, "%Q")) |> # create
a new variable for the quarter
group_by(quarter) |> # group by the quarter variable
summarise(q_ipc = mean(ipc)) |>
mutate(q_inf = ((q_ipc/dplyr::lag(q_ipc))-1)*100) |>
slice(-1)
# A tibble: 157 x 3
quarter q_ipc q_inf
<yearqtr> <dbl> <dbl>
1
1984 Q2 1.49 5.66
2
1984 Q3 1.59 6.53
3
1984 Q4 1.76 11.0
4
1985 Q1 2.11 19.6
5
1985 Q2 2.24 6.43
6
1985 Q3 2.32 3.53
7
1985 Q4 2.41 3.67
8
1986 Q1 2.44 1.23
9
1986 Q2 2.39 -2.01
10 1986 Q3 2.42
1.40
# ... with 147 more rows
Ahora, definimos una inflación trimestral como una serie temporal usando la función ts.
ts_data <- ts(q_dataset$q_inf, start
= c(1984,2), frequency = 4)
Qtr1 Qtr2 Qtr3 Qtr4
1984 5.66392672 6.52527285 10.99767476
1985 19.64583811 6.43449238
3.53425010 3.66683217
1986
1.23093134 -2.00846916
1.39780793 4.35942001
1987
1.45783902 4.75590834 5.30846177
6.77347683
Ahora, usamos la función stl (ver referencia: https://otexts.com/fpp2/stl.html) para obtener una descomposición de la serie, recuperando los componentes estacionales, la tendencia y el componente aleatorio de las series.
# Decompose the time series using the
STL function
decomp <- stl(ts_data, s.window =
"periodic")
# Extract the seasonal, trend, and
remainder components
seasonal <- decomp$time.series[,
"seasonal"]
trend <- decomp$time.series[,
"trend"]
remainder <- decomp$time.series[,
"remainder"]
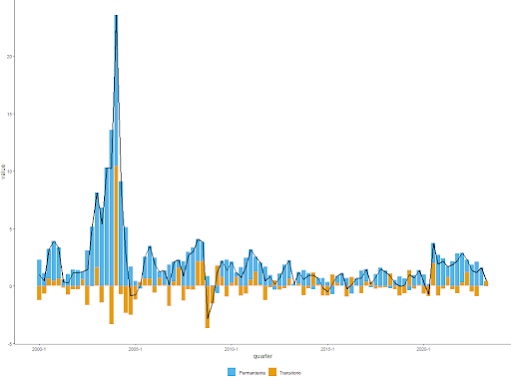
Ahora, agregamos los componentes (remainder) transitorios vs. permanentes (trend + seasonal).
q_dataset$permanent <- trend +
seasonal
q_dataset$transient <- remainder
# A tibble: 157 x 5
quarter q_ipc q_inf permanent
transient
<yearqtr> <dbl> <dbl> <dbl> <dbl>
1
1984 Q2 1.49 5.66
5.67 -0.00924
2
1984 Q3 1.59 6.53
8.72 -2.19
3
1984 Q4 1.76 11.0 10.7
0.325
4
1985 Q1 2.11 19.6 11.4
8.23
5
1985 Q2 2.24 6.43
8.27 -1.83
6
1985 Q3 2.32 3.53
5.81 -2.28
7
1985 Q4 2.41 3.67
3.29 0.376
8
1986 Q1 2.44 1.23
1.57 -0.340
9
1986 Q2 2.39 -2.01 -0.0908
-1.92
10 1986 Q3 2.42
1.40 1.39 0.00589
# ... with 147 more rows
Finalmente, se crea un gráfico apilado asumiendo la incidencia de cada componente.
q_dataset |>
dplyr::filter(quarter >= "2000 Q1") |>
gather(id, value, -c(quarter,q_ipc,q_inf)) |>
ggplot(aes(x = quarter, y = value, fill = id)) +
geom_bar(stat = "identity") +
scale_fill_manual(values = c("#56B4E9", "#E69F00"),
name = element_blank(), labels = c("Permantente",
"Transitorio")) +
geom_line(aes(x = quarter, y = q_inf), size=0.8) +
theme_classic() +
theme(legend.position = "bottom")
Sin embargo, vemos que la metodología anterior asume los componentes estacionales como transitorios. Por lo que, la política monetaria estaría reaccionando a elementos estacionales al considerarlos como elementos permanentes, sin embargo, entendemos que este elemento debe agregarse como elemento transitorio.
