Ejemplo
1: Búsqueda de factores mediante el método de regresión unifactorial
Entre la familia de modelos
factoriales, un método de búsqueda de factores consiste en seleccionar como
factor aquellas variables que maximizan el R-cuadrado ponderado por la varianza
de la variable dependiente, dentro de un conjunto de posibles variables
(Novales, 2015). En este primer ejemplo, se utiliza una matriz de 1,000
variables aleatorias (ncol=1000) simuladas con una distribución
normal, cada una de las cuales tiene 100 observaciones (nrow = 100)
y posteriormente se busca entre las restantes 999 variables, cual de esta es la
que regresa mayor R^2 ponderado por la varianza de las variables independiente.
> mydata<-matrix(rnorm(1000*100),
ncol=1000, nrow = 100)
> c<-1
> guarda<-numeric()
> for(i in
2:ncol(mydata)) {
+ guarda[c]<-r2<-summary(lm(mydata[,1]~mydata[,i]))$r.squared*var(mydata[,i])
+
c<-c+1
+ }
> (n<-which(guarda==max(guarda))+1)
[1] 499
> (Rmax<-guarda[n])
[1] 0.03195229
Entendiendo el funcionamiento global
del código, lo explicaremos paso a paso:
1. Se
accede al conjunto de datos [mydata<-matrix…]
2. Posteriormente
se crea un contador () que nos ayudará a ir accediendo a los elementos del
vector donde guardaremos los resultados (verifique que esto lo puedes realizar
con el mismo contador del bucle, colocando i-1)
y un vector vacío donde pretendemos ir guardando los R2 ponderados que vamos
obteniendo.
3. Luego,
con la ayuda del bucle for -aunque debe quedar claro que este problema puede
resolverse fácilmente sin la ayuda de bucles utilizando el cuadrado de la
matriz de correlación de los datos (demuéstrelo)- realizamos lo siguiente:
a.
Creamos un bucle for
con un índice o variable de control (i) que sigue una secuencia que va desde 2
hasta el número de columna (variables) existente en mi matriz de datos [for(i in 2:ncol(mydata))].
Esta variable control es del tipo local y tiene como objetivo recorrer las
variables de la matriz de datos para ser incluidas en el modelo de regresión
b.
Luego, anidamos varias
funciones en un mismo comando (cuestión no recomendada si estas iniciando el
uso de R). Primero, utilizamos la función lm para
estimar el modelo de regresión [lm(mydata[,1]~mydata[,i])]:
la clave aquí es utilizar la estructura normal de la función lm(y~x), donde la
variable x se mantiene fija lm(mydata[,1],
mientras que mediante indexación utilizamos el índice del bucle para ir
cambiando la variable x en cada iteración del bucle [mydata[,i]].
Así, dado lo explicado en el punto a, este tomará el valor de 2,3,4,5,6,…,ncol
con cada repetición.
c.
En esta misma línea de
comando, se utiliza el comando para obtener el R2 de la regresión estimada [summary(modelo)$r.squared],
multiplicándose este por la varianza de la variable independiente [var(mydata[,i])].
Así, toda la expresión nos permite obtener el R2 ponderado por la varianza.
summary(lm(mydata[,1]~mydata[,i]))$r.squared*var(mydata[,i])
d.
El resultado obtenido,
se guarda en un vector llamado guarda,
a cuyas posiciones se accede mediante indexación, utilizando la figura del
contador, pues en la primera iteración del bucle, este tiene el valor de 1 [c<-1],
por lo que se accede a esta posición del vector, pero con cada secuencia, este
valor se va incrementando en una unidad [c<-1].
Reiteramos, este no era necesario, solo se incluye para explicar un posible uso
del mismo, porque observe que en cada “vuelta” del bucle, c=i-1.
4. Finalmente,
se utiliza la instrucción wich
para acceder a la posición del vector guarda donde está el máximo valor de los r2
estimados [which(guarda==max(guarda))],
pero recordemos, que en la primera posición se ha guardado del r2
correspondiente a la regresión a la variable 1 con la 2, en la segunda posición
de la 1 con la 3, en la tercera 1 con 4, …, hasta en la posición m esta la
relación 1 con la m+1, por lo que, si queremos averiguar cuál fue la variable
donde se obtiene el mayor r2, debemos acceder a la posición donde queda el
máximo + 1 [(n<-which(guarda
== max(guarda)) +1)]
para obtener la posición de la variable que arrojo el mayor r2.
5. Finalmente,
se utiliza el valor n
de esta variable, para verificar cual fue la variable que representó el mayor
R.
6. Una
extensión directa a este método, para el caso de dos variables, seria
transformar el vector guarda
en una matriz. Inténtelo.
Ejemplo
2: Estimación de la distribución empírica del promedio mediante Bootstrap
(Ejemplo trabajado a partir del Repositorio
de educación superior del Ec) Dada una
muestra de N=10.000 observaciones para una variable y, tomar una sub-muestra (1)
aleatoria M<N, por ejemplo 40, y calcular la media para la sub-muestra con
remplazamiento [sample(xmuestra, size=40, replace = TRUE)].
(2) Repetir el procedimiento 1000 veces [for(i in 1:1000)]. Finalmente,
Estas 1.000 réplicas de la media [mean(x2)] para cada sub-muestra
representan la distribución (empírica) del estimador.
> xmuestra<-rnorm(1000)
> xbootstrap<-c()
>
> for(i in 1:1000) {
+ x2<-sample(xmuestra, size=40, replace =
TRUE)
+ xbootstrap<-c(xbootstrap, mean(x2))
+ }
> hist(xbootstrap)
> abline(v = mean(xbootstrap), col =
"blue", lwd = 2)
Aquí se modifica la forma en cómo
se guarda el vector, en vez de indexación como se utilizó en el ejemplo 1, se
van concatenando vectores mediante [xbootstrap<-c(xbootstrap,
mean(x2))]. Observe como opera este comando
de forma secuencial: durante la primera iteración del bucle, xbootstrap es un vector vacío,
que se concatena con la media de la primera sub-muestra que acabamos de obtener
y se guarda en un vector con el mismo nombre; en la segunda iteración, xbootstrap es un vector con la media de la primera
sub-muestra y se concatena con la media de la segunda sub-muestra, por lo que,
en la tercera corrida del bucle este vector (xbootstrap)
contiene los dos primeros promedios, correspondiente a las dos primeras muestra
y se concatena con la tercera media, así sucesivamente hasta repetir el procedimiento
mil veces.
Ejemplo
3: Modelos factoriales, establecer criterios de búsqueda
Ahora retomamos el ejemplo 1, pero
en esta ocasión, en vez de realizar todas las regresiones solo queremos repetir
el ejercicio hasta encontrar un R^2 superior a 0.1, suponiendo el caso que solo
queremos encontrar una variable que explique nuestra variable dependiente con
suficiente precisión. (1) Observe que colocamos r2=0 [R2 <- 0],
para poder iniciar el criterio de búsqueda colocado en el bucle while [while(R2 <
0.1)]; (2) luego utilizamos la figura del
contador (i) para ir recorriendo mi matriz de datos variable por variable mydata[,i+1] (como
anteriormente se pudo utilizar desde 2 hasta n, pero se modifica para ilustrar
otro ejemplo de cómo utilizar los bucles.); (3) guardamos el R2 de esta
regresión [R2<-summary(lm(mydata[,1]~mydata[,i+1]))$r.squared]
para verificar si este cumple con el criterio de parada establecido en el
bucle, en caso negativo la secuencia sigue realizándose, mientras que en caso
contrario la misma se detiene.
> R2 <- 0
> i <-1
>
> while(R2 < 0.1) {
+ R2<-summary(lm(mydata[,1]~mydata[,i+1]))$r.squared
+ i<-i+1
+ }
> i
[1] 499
Una alternativa seria buscar en el
vector llamado guarda,
donde se colocaron todos los R2 del ejemplo 1, y buscar en este el primer valor
superior a 0.1, para verificar cual variable cumple con el criterio en primer
lugar, pero esto requeriría realizar todas las estimaciones, que es lo que se
quiere evitar en este ejemplo.
Además, este ejemplo se puede
extender al caso de gestión de carteras, en econometría financiera, solo cambiamos
el criterio de búsqueda. Por ejemplo, buscar series que cointegren para la
búsqueda de carteras replicas, que muestren transferencias en volatilidad o que
muestren betas parecidos para la réplica del riesgo de carteras. También al
caso de políticas macroeconómicas de buscar entre un conjunto de variables,
aquellas que muestren causalidad sobre otro grupo.
Por último, una nota aclaratoria es
que podemos incurrir en bucles infinitos cuya condición de parada no se cumpla
nunca, por tanto, por ejemplo [while(R2 < 1)]
(pero en el ejemplo anterior, que pasaría si coloco esta condición de parada,
obtendría un error? Cree intencionalmente un bucle infinito?). En casos de
bucles infinitos podemos detenerlos en R mediante Ctrl+c.
Ejemplo
4: Econometría Financiera: estimación de momentos mediante ventanas móviles
En este cuarto ejemplo, utilizamos
datos sobre el precio del oro para estimar la volatilidad histórica del mismo
utilizando el concepto de ventanas móviles (Novales, 2013). La idea de este
procedimiento es representar los cambios en un determinado momento, que sufren
las series a través del tiempo. Para esto, la n primeras
observaciones de una serie (donde n se llama ventana) y se estima sobre esta
ventana el momento deseado, posteriormente se accede a una segunda ventana
donde se descarta la primera observación de esa ventana y se agrega una nueva
observación, y así sucesivamente hasta recorrer todas las observaciones
disponibles de la serie. La estimación de cada ventana se guarda
secuencialmente y se obtienen una representación histórica de la misma.
a. Se
cargan los datos y se calcula la rentabilidad del precio [diff(log(oro))],
por las razones econométricas comunes.
b. Luego
se crea un bucle [for (i in 1:T-26) {]
que permite recorrer las observaciones del vector de rentabilidades del oro,
por medio de una ventana de 26 observaciones, hasta alcanzar T [T<-
length(roro)], que es la longitud de la serie
considerada.
c.
Luego, se utiliza
indexación para acceder a la parte del vector de rentabilidades que nos
interesa para obtener su desviación estándar [sd(roro[i:(i+25)]].
d. Las
volatilidades estimadas se guardan mediante concatenación de resultados, como
se hizo en el ejemplo 2 [c(wvol,sd(roro[i:(i+25)]))].
e.
Posteriormente se
indica que este vector corresponde a una serie temporal, mediante el comando ts y se obtiene una representación de las
mismas.
> rm(list = ls(all.names = TRUE))
> setwd("C:/Users/nramirez/Dropbox/Econometria
I PCMM/Datos")
>
> poro <-
read.delim("Data_precio_oro.txt")
> attach(poro)
> # calcula rentabilidad
> roro<-diff(log(oro))
> T<- length(roro)
> wvol<-c()
> for (i in 26:T) {
+ wvol<-c(wvol,sd(roro[i:(i+25)]))
+ }
> RentOro<-ts(wvol,
start=c(1991,4,4), frequency = 252)
> plot(RentOro, t='l',
col='blue')
Ejemplo
5: Econometría Financiera: representación histórica del riesgo sistemático de
un activo (riesgo beta)
Dado un modelo unifactorial, se
utiliza el método de ventanas móviles para obtener los betas correspondiente a
cada periodo y posteriormente representar este beta, lo que se conoce en la
literatura como la representación histórica del riesgo sistemático de un activo.
En este caso se utiliza la misma filosofía utilizada en el ejemplo anterior,
moviendo el segmento de datos utilizados para estimar el modelo factorial [[i:(i+125)]].
Posteriormente, accedemos al coeficiente estimado [$coefficients[2]],
guardamos el coeficiente correspondiente a cada uno de los modelos considerados
y representamos esta serie histórica.
> beta<-c()
> for (i in 1:(length(dlnCisco)-126)) {
+ beta1<-lm(dlnCisco[i:(i+125)]~dlnSP100[i:(i+125)])$coefficients[2]
+ beta<-c(beta, beta1)
+ }
>
> tsbeta<-ts(beta, start=c(2000,6,20),
frequency = 252)
> plot(tsbeta, type="l")
[Este ejemplo se puede modificar fácilmente para
obtener una estimación recursiva,
modificando la secuencia del bucle [for (i in 126:length(dlnCisco))] y la
indexación de la variable utilizada [[1:i]].
Ejemplo
6: Representación de variables aleatorias
Simula distintos valores de y,
cuando esta sigue una distribución binomial, obtenemos un histograma de una
binomial alterando mediante un bucle los posibles valores de la variable
aleatoria.
> n=10; p<-0.1; py<-0;
> for (y in 0:10) {
+ py[y+1]<-(factorial(n)/(factorial(y)*factorial(n-y)))*(p^y)*((1-p)^(n-y))
+ }
> barplot(py,beside=FALSE)
Nota: tenga pendiente que
utilizando el EJEMPLO 3.7 el libro de estadística matemática con aplicaciones
se verifica que [(factorial(n)/(factorial(y)*factorial(n-y)))*(p^y)*((1-p)^(n-y))]
es igual a la función pbinom
de r. Por ejemplo, suponga que un lote de 5000 fusibles eléctricos contiene 5%
de piezas defectuosas. Si se prueba una muestra de 5 fusibles, encuentre la
probabilidad de hallar al menos uno defectuoso.
> n=5;
p<-0.05; y<-0;
> 1-(factorial(n)/(factorial(y)*factorial(n-y)))*(p^y)*((1-p)^(n-y))
[1] 0.2262191
> 1-pbinom(0,5,.05)
[1] 0.2262191
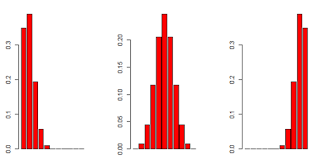
Ejemplo
7: Representación de variables aleatorias usando bucles anidados
[Tomado del libro de estadística
matemática con aplicaciones] Construya histogramas de probabilidad para las
distribuciones de probabilidad binomiales para n = .5, p = .1, .5 y .9. Nótese
la simetría para p = .5 y la dirección del sesgo para p = .1 y .9.
Ahora, como necesitamos simular
varias variables aleatoria, cambiando el valor de y como hicimos en el ejemplo
anterior, necesitaremos además modificar el parámetro p en la función de distribución
binomial. Entonces, necesitamos simular una variable aleatoria para cada valor
de este parámetro.
> n=10; p<-0.1; py<-0;
> for (y in 0:10) {
+ py[y+1]<-(factorial(n)/(factorial(y)*factorial(n-y)))*(p^y)*((1-p)^(n-y))
+ }
> barplot(py,beside=FALSE)
> #------------------------------------
> n=10; py<-0; a<-matrix( ,nrow=11,
ncol=1)
> par(mfrow=c(1,3))
>
> for (p in c(0.1, 0.5, 0.9)){
+ for (y in
0:10) {
+ py[y+1]<-(factorial(n)/(factorial(y)*factorial(n-y)))*(p^y)*((1-p)^(n-y))
+ }
+ a<-cbind(a,py)
+ barplot(a[
,ncol(a)],beside=FALSE,type="l",col="red")
+ }