La volatilidad de las series financieras y económicas es un momento (característica) indispensable para caracterizar cualquier serie. Usualmente esta mide el nivel de fluctuaciones de una serie alrededor de una medida de referencia, por lo general, la media. Por lo que, una mayor varianza generalmente esta asociada a mayor incertidumbre de los datos. En aplicaciones puntuales, indican que la volatilidad del retorno de un activo financiero se asocia con su precio; la volatilidad del tipo de cambio se asocia al uso de instrumentos de cobertura por parte de los agentes del mercado; la volatilidad de la inflación resta capacidad de pronósticos por los interesados; igual mayor incertidumbre en la actividad económica puede llevar a las instituciones financieras a tomar mayores precauciones frente a posibles eventos adversos, incidiendo inclusive en posibles caídas del consumo… En todos los casos, la volatilidad tiene una incidencia directa sobre las decisiones económicas y las características de las series.
En este marco y entendiendo que la incertidumbre alrededor de la serie es una condición latente (no observable), surgen diferentes alternativas para su medición. La primera de estas alternativas corresponde a la volatilidad incondicional de la serie estacionaria[1]. La estacionariedad de la serie suele aproximarse a partir de la primera diferencia logarítmica, que en finanzas se les llaman retornos.
data("EuStockMarkets")
as.data.frame() |>
mutate(DAX_Return = log(DAX) - log(dplyr::lag(DAX))) |>
select(DAX_Return)
[1] 0.01030084
Volatilidad incondicional
A partir de la varianza de la primera diferencia logarítmica de la serie hemos obtenido la desviación estándar incondicional como primera aproximación de la volatilidad de la serie en cuestión. Ahora bien, una simple inspección del grafico de esta serie (1ra diferencia logarítmica), nos lleva aprecios que el grado de las fluctuaciones de las series respecto al nivel de referencia tiende a cambiar en el tiempo.
library(ggplot2)
ggplot(df, aes(x = time(EuStockMarkets), y = DAX_Return)) +
geom_line()
+
theme_minimal()
Si estimáramos la varianza en dos lugares distintos de
nuestra muestra de datos, obtendríamos valores diferentes.
sd(dln_dax$DAX_Return[900:1000], na.rm = TRUE)
Bajo estas condiciones, ha sido ampliamente documentado en la literatura que esta media suele enfrentar inconvenientes asociados a:
i.
Considera la volatilidad como un fenómeno estable en el
tiempo.
ii.
Reconoce como volatilidad cambios de nivel en la serie o
presencia de tendencias.
iii.
No reconoce que parte de las fluctuaciones de una serie
podrían ser anticiparles (en caso de serlo no se entiende como volatilidad).
iv. Es una medida que mira hacia el pasa.
Ventana de volatilidad
Estas debilidades han llevado a considerar algunas medias alternativas de volatilidad. La primera de estas medidas es la media móvil. Esta consiste en seleccionar una ventana temporal (por ejemplo 20 observaciones) e ir calculando la volatilidad en cada ventana temporal, de forma tal, que se obtenga una medida de la volatilidad histórica. Por ejemplo: tomamos las primeras 20 observaciones, luego tomamos de la observación 2:21, 3:22, … hasta recorrer toda la muestra. Esto permite obtener un vector de volatilidades.
window_size <- 66
r_dax <- dln_dax$DAX_Return[-1]
volatility_window <- rollapply(r_dax, width = window_size,
FUN = sd, align = "right", fill = NA)
dln_dax$H_vent_vol <- c(NA,volatility_window)
Note como ahora se esta considerando la volatilidad como un momento cambiante en el tiempo:
geom_line() +
geom_hline(yintercept = sd(dln_dax$DAX_Return, na.rm = TRUE),
col = "red", linetype = "dashed") +
Ponderación exponencial
Sin embargo, las ventanas de volatilidad también suelen presentar debilidades importantes asociadas a que no es trivial seleccionar la amplitud deseada de la ventana de estimación, en el sentido de que ventanas muy pequeñas sueles ser bastante sensible al nuevo dato observados, mientras que al usar ventanas más grandes la serie tiende a suavizarse. Por tanto, la amplitud de la ventana dependerá de cual entendamos modela mejor las características de las series. Otra debilidad es que pondera por igual todas las observaciones de nuestra base, cuando entendemos que los valores recientes guardan mayor cantidad de información. Ambas debilidades son enfrentadas por un modelo de exponenciación exponencial, que permite brindar mayor ponderación a las observaciones recientes, además salta el problema de la selección de ventana.
varEWMA<- var(r_dax, na.rm=TRUE);
lambda<-0.94
for (t in 2:(tobs + 1)) {
varEWMA[t]<-lambda*varEWMA[t-1]+(1-lambda)*(r_dax[t-1]^2)
#no consideramos la primera obs
}
dln_dax$H_Ewma <- sqrt(varEWMA)
dln_dax %>%
select(starts_with("H_")) |>
mutate(fecha= time(EuStockMarkets)) |>
pivot_longer(cols = -fecha, names_to = "variable", values_to = "valor") |>
ggplot(aes(x = fecha, y = valor, color = variable)) +
geom_line() +
theme_minimal()
Modelos GARCH
Adicional a las alternativas anteriores, buscando modelar regularidades empíricas observadas alrededor de las seréis económicas y financieras, se han agregado los modelos GARCH, estos modelos son una generalización de los modelos ARCH y permiten modelar temas como reversión a la media. Capacidad para modelar patrones de volatilidad a largo plazo: Los modelos GARCH son más adecuados para modelar patrones de volatilidad a largo plazo, lo que significa que pueden adaptarse mejor a la evolución de la volatilidad en el tiempo. En R, el paquete rugarch permite estimar este tipo de modelos.
spec <- ugarchspec(variance.model = list(model = "sGARCH",
garchOrder = c(1, 1)))
fit <- ugarchfit(spec, data = r_dax)
volatility <- sigma(fit)
dln_dax$H_garch <- c(NA, volatility[,1])
dln_dax %>%
select(starts_with("H_")) |>
mutate(fecha= time(EuStockMarkets)) |>
pivot_longer(cols = -fecha, names_to = "variable", values_to = "valor") |>
ggplot(aes(x = fecha, y = valor, color = variable)) +
geom_line() +
theme_minimal()
Modelos ARMA-GARCH no gaussiano
Extensiones del modelo GARCH han permitido incorporar no normalidades (por ejemplo, usando distribución t, que permite incorporar colas más pesas que indican que los eventos extremos se hacen más posibles); asimetrías en la respuesta en volatilidad (modelos gjr-garch que indican que las noticias positivas/negativas tendrán un efecto diferenciados; o modelar conjuntamente correlaciones en el nivel de la serie estacionaria, mediante los conocidos arma-garch.
garchOrder = c(1, 1)),
mean.model = list(armaOrder = c(1, 1)),
distribution.model = "std")
fit2 <- ugarchfit(spec, data = r_dax)
volatility2 <- sigma(fit2)
dln_dax$H_gjr_t <- c(NA, volatility2[,1])
dln_dax %>%
select(starts_with("H_")) |>
mutate(fecha= time(EuStockMarkets)) |>
pivot_longer(cols = -fecha, names_to = "variable", values_to = "valor") |>
ggplot(aes(x = fecha, y = valor, color = variable)) +
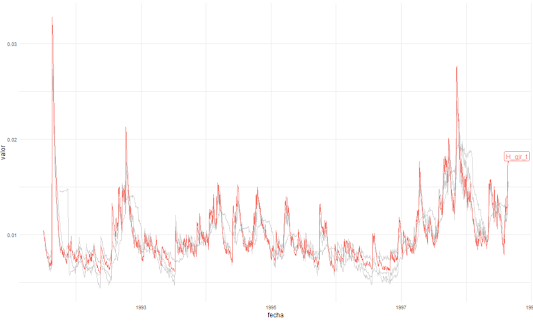
gghighlight(variable=="H_gjr_t")
Finalmente, otras alternativas de los modelos de volatilidad provienen de los modelos de volatilidad estocástica.
library(stochvol)res <- svsample(r_dax, priormu = c(-10, 1), priorphi = c(20, 1.1), priorsigma = .1)
summary(res, showlatent = FALSE)
dln_dax$H_stoc_v <- c(NA, res$summary$sd[,"mean"])
dln_dax %>%
select(starts_with("H_")) |>
mutate(fecha= time(EuStockMarkets)) |>
pivot_longer(cols = -fecha, names_to = "variable", values_to = "valor") |>
ggplot(aes(x = fecha, y = valor, color = variable)) +
geom_line() +
theme_minimal() +
gghighlight(variable %in% c("H_gjr_t","H_stoc_v"))
[1] Recuerde que el uso de momentos solo se justifica en
casos donde la serie estimada sea estacionaria. Por ende, al medir la volatilidad
de una serie temporal, debemos testear previamente el orden de integración de
la serie, pasa saber si necesitamos realizar alguna transformación previa antes
de estimar la volatilidad.