library(tidyverse)
library(readxl)
library(xts)
datos
<- read_excel("~/food_index_fred.xls",
col_types =
c("date", "numeric"))
head(datos)
# A
tibble: 6 x 2
observation_date PFOODINDEXM
<dttm> <dbl>
2 1992-02-01 00:00:00 57.8
3 1992-03-01 00:00:00 57.5
4 1992-04-01 00:00:00 56.2
5 1992-05-01 00:00:00 57.7
6 1992-06-01 00:00:00 57.3
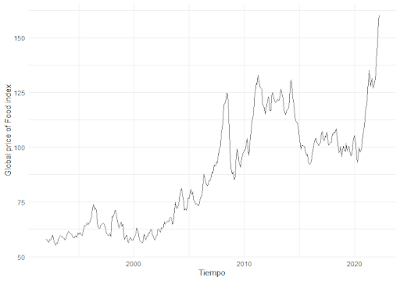
Vamos la evolución histórica de la serie. Declaramos que la serie es un objeto temporal a partir del paquete xts y usando el índice de precios. Esta definición es especialmente útil cuando trabajamos con datos diarios o donde la secuencia de fecha asociada no es x-distantes en el tiempo.
#
asignando representation de una serie temporal
ts_food
<- xts(x = datos$PFOODINDEXM, order.by = datos$observation_date)
autoplot(ts_food)
+
theme_minimal() +
labs(y = "Global price of Food
index", x = "Tiempo")
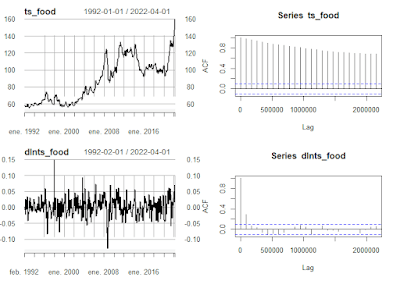
Estimamos el correlograma. Si los coeficientes están dentro del intervalo de confianza, no rechazamos la hipótesis nula de que estos sean iguales a cero. En caso contrario rechazamos. Claramente quedan fuera, por lo que, no rechazamos la hipótesis nula. Cuando rechazamos (están fuera del intervalo) decimos que la serie presenta autocorrelación.
Ahora obtenemos una representación de las series en niveles y sus diferencias (se transforma en logaritmo porque ayuna a cumplir supuestos como estabilidad de varianza, y permite que la diferenciación se puede interpretar como una tasa de variación que no depende de las unidades de escalas).
#
Obtener cambio logaritmico
dlnts_food
<- diff(log(ts_food))[-1]
par(mfrow=c(2,2))
plot(ts_food)
acf(ts_food)
plot(dlnts_food)
acf(dlnts_food)
Estimamos la estrategia ARIMA. En el siguiente ejemplo se estima un ARIMA para una serie integrada de primer orden (suponemos solo se necesita una diferenciación para obtener una serie estacionaria) de orden 1,1, para los coeficientes AR y MA, respectivamente. El primer número corresponde al AR, el segundo al orden de integración de la serie y el tercero al MA.
#
estimacion ARIMA
model1
<- arima(ts_food,order=c(1,1,1)
model1
Call:
arima(x
= ts_food, order = c(1, 1, 1))
Coefficients:
ar1
ma1
0.313
0.058
s.e. 0.174
0.188
sigma^2
estimated as 6.69: log likelihood =
-860, aic = 1726
Evaluación del modelo. La evaluación se hace recuperando los residuos y verificando estos no tienen autocorrelación o no están asociado con ninguna otra variable. En caso contrario podría apuntar a que se omite información o que no se está modelando correctamente la estructura de la serie. Note en el siguiente correlograma que todos los valores están dentro, por tanto, no rechazamos la hipótesis nula de que estos sean iguales a cero. Aceptamos el modelo. En caso de que estos estén fuera apunta a que necesitamos otra alternativa para modelarlo.
acf(r)
Una alternativa de evaluación de la autocorrelación de las series se obtiene del test de Box. Cuya hipótesis nula es que estos coeficientes son iguales a cero. En ambos casos se obtienen p-valor elevados (mayor al valor critico seleccionado), esto hace que no se rechace la hipótesis nula asociada al test, por tanto, decimo que la serie no presenta autocorrelación.
Box.test(r,lag=1,type
= "Box-Pierce")
Box-Pierce test
data: r
X-squared
= 0.011, df = 1, p-value = 0.9
Box.test(r,lag=1,type
= "Ljung-Box")
Box-Ljung test
data: r
X-squared
= 0.011, df = 1, p-value = 0.9
Uso del modelo. El modelo se puede usar para predecir o descomponer la evolución de la serie en una parte sistemática y otra no (clave en la gestión del riesgo). Predict nos permite recuperar la predicción y el error estándar de dicho error.
predict(model1,n.ahead=12)
$pred
Time
Series:
Start =
31449601
End =
32400001
Frequency
= 0.0000115740740740741
[1] 160.9 161.1 161.2 161.2 161.2 161.2 161.2
161.2 161.2 161.2 161.2 161.2
$se
Time
Series:
Start =
31449601
End =
32400001
Frequency
= 0.0000115740740740741
[1]
2.586 4.389 5.836
7.042 8.084 9.010
9.851 10.625 11.347 12.026
[11]
12.669 13.280
Finalmente, recuerde que la función auto.arima de R, permite identificar este tipo de modelos.