En la siguiente entrada se muestran algunos ejemplos de cómo realizar test
de independencia estadística en R, para responder a uno de los ejercicios de la asignatura de Seminario de Investigación (clase 6 de la parte de R). Los ejercicios se realizan con la base utown del libro Principles of Econometrics 4e, by Carter Hill, William Griffiths,
and Guay Lim. Los mismos se encuentran disponibles en el paquete PoEdata.
library(PoEdata)
library(tidyverse)
data(utown)
head(utown,5)
## price
sqft age utown pool fplace
## 1 205.452 23.46
6 0 0
1
## 2 185.328 20.03
5 0 0
1
## 3 248.422 27.77
6 0 0
0
## 4 154.690 20.17
1 0 0
0
## 5 221.801 26.45
0 0 0
1
1. Análisis de independencia
1.1. Usando ggplo2, presente un histograma de precios y muestre un summary
(min, max,median, q1, q5) condicionado a si la casa tiene o no piscina (pool).
theme_set(theme_minimal())
#histograma
utown%>%
ggplot(aes(price)) +
geom_histogram(col = "black",fill = "darkblue", alpha = 0.6)
# Summary de precios por grupo
tapply(utown$price, utown$pool, summary)
##
$`0`
## Min. 1st
Qu. Median Mean 3rd Qu. Max.
## 134.3 214.8
244.3 246.5 276.8
345.2
##
## $`1`
## Min. 1st
Qu. Median Mean 3rd Qu. Max.
## 160.3 219.5
249.1 252.0 285.4
340.7
1.2. Obtenga un boxplot donde relacione el tener piscina o no, con el
precio de la casa, y establezca la independencia entre las variables.
utown%>%
ggplot(aes(y=price, x=factor(pool), fill=factor(pool))) +
geom_boxplot(col = "black", alpha = 0.6)
1.3. A partir de la comparación de promedios, que conclusión podemos
obtener y que limitaciones puede enfrentar esta conclusión sobre la posible
obtención de un efecto causal.
Al considerar los intervalos del gráfico anterior se puede observar que los
promedios son relativamente parecidos, sin embargo, esta comparación no se
puede interpretar como un efecto causal, dado que esta simple comparación omite
otros factores relevantes que inciden sobre el precio de las casas.
1.4. Presente una tabla de frecuencia, donde los porcentajes se presenten
en relación a las tablas, interprete sus resultados y posteriormente realice el
test chi2 para determinar la posible independencia entre las variables.
Necesitamos una tabla de frecuencia de precio con pool, pero price es una
variable continua, por lo que, debemos discretizarla, antes de realizar la
tabla de frecuencia. Una alternativa es crear rangos de precios (cut(price,
breaks = 5)), utilizar los quintiles (ejemplo debajo), o separarla en grupos
alrededor de alguna medida como la media (price>mean(price)).
# discretizar la variable precio
utown <- utown %>%
mutate(quintiprecio = ntile(price, 5))
utown %>%
select(quintiprecio, pool) %>%
table() %>%
prop.table(.,2)
## pool
## quintiprecio
0 1
## 1
0.2085427 0.1666667
## 2
0.2010050 0.1960784
## 3
0.1959799 0.2156863
## 4
0.2022613 0.1911765
## 5
0.1922111 0.2303922
Los valores son bastante diferentes, eso es evidencia de independencia,
pero se debe realizar el test chi2 de independencia entre variables discretas (p.valor=0.5508, no se rechaza ho de independencia):
# discretizar la variable precio
utown %>%
select(quintiprecio, pool) %>%
table() %>%
chisq.test()
##
## Pearson's
Chi-squared test
##
## data: .
## X-squared = 3.0422, df = 4, p-value = 0.5508
2. Análisis de independencia: Correlación
2.1. Sabiendo que tenemos una medida del size del terreno de la casa
(sqft), crear los quintiles de esta variable y muestre una tabla resumen donde
indique el precio max, min, mediano, q1 y q3 del precio de las casas para cada
quintil.
utown %>%
mutate(quintiprecio = ntile(price, 5)) %>%
select(price,quintiprecio) %>%
group_by(quintiprecio) %>%
summarise(min = min(price),
q1 = quantile(price,0.2),
mean = mean(price),
q3 = quantile(price,0.6),
max = max(price))
## # A tibble: 5 x 6
##
quintiprecio min q1
mean q3 max
##
<int> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1
1 134. 178.
190. 197. 208.
## 2
2 209. 214.
222. 225. 235.
## 3
3 235. 239.
246. 249. 258.
## 4
4 258. 263.
272. 274. 287.
## 5 5
287. 293. 309.
311. 345.
2.2. Obtenga un scatter donde relacione el size de la casa con el precio,
interprete los resultados, coloreando los puntos según la casa tenga o no
piscina (pool).
utown %>%
ggplot(aes(sqft, price, color =factor(pool)))+
geom_point()+
geom_smooth()
2.3. Realice el test de correlación de pearson y determine si rechaza o no
ho.
Se rechaza ho.
cor.test(utown$price,utown$sqft, method
= "pearson")
##
## Pearson's
product-moment correlation
##
## data:
utown$price and utown$sqft
## t = 23.367, df = 998, p-value < 2.2e-16
## alternative hypothesis: true correlation is not
equal to 0
## 95 percent confidence interval:
## 0.5530750
0.6333235
## sample estimates:
## cor
## 0.5946785
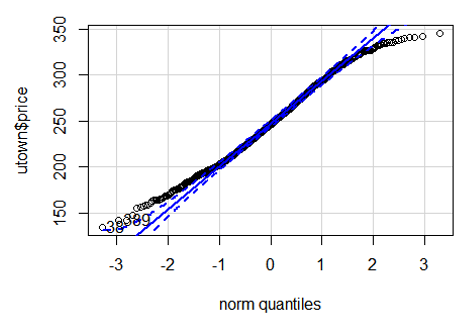
2.4. Utilice el qqplot para realizar un test de normalidad sobre el price y
sqft.
car::qqPlot(utown$price)
2.5. En base al test de normalidad, que podemos concluir sobre las medidas
de resumen y el análisis de correlación realizado.
Como para las colas se rechaza que la variable se comporte como una normal,
se entiende que es preferible usar alguna estimación no parámetrica para
obtener el coeficiente de correlación, tal como el método de Spearman.
3. Test de media
3.1. Realice un test de media para testear si las casas con chimeneas son estadísticamente más grandes que aquellas casas que no tienen.
t.test(sqft~fplace,
data=utown,
var.equal=F,
alternative = "greater",
conf.level=0.95)
##
## Welch Two
Sample t-test
##
## data: sqft
by fplace
## t = -3.1236, df = 989.19, p-value = 0.9991
## alternative hypothesis: true difference in means is
greater than 0
## 95 percent confidence interval:
##
-0.8778771 Inf
## sample estimates:
## mean in group 0 mean in group 1
##
24.91187 25.48674
3.2. Realice boxplot donde compare el precio de la casa según el size esté
por encima o por debajo de la mediana.
utown%>%
mutate(sqftmedian = sqft>median(sqft)) %>%
ggplot(aes(y=price, x=factor(sqftmedian), fill=factor(sqftmedian))) +
geom_boxplot(col = "black", alpha = 0.6)
3.3. Realice un test de media para testear si las casas con edad por encima
de la mediana, tienen a tener un precio menor al resto de casa.
utown
<- utown %>%
mutate(medianEdad = as.numeric(age>median(age)))
t.test(price~medianEdad,
data=utown,
var.equal=F,
alternative = "less",
conf.level=0.95)
##
## Welch Two
Sample t-test
##
## data: price
by medianEdad
## t = 1.2334, df = 994.12, p-value = 0.8911
## alternative hypothesis: true difference in means is
less than 0
## 95 percent confidence interval:
## -Inf
7.685081
## sample estimates:
## mean in group 0 mean in group 1
##
249.2916 246.0001