En
la siguiente entrada se utilizan datos sobre el PIB per cápita en dólares,
disponibles en la CEPAL, para los países
latinoamericanos, con la intención de mostrar algunas peculiaridades del
crecimiento económico en la región, utilizando los paquetes dplyr y ggplot2 de tidyverse (es pre-requisito conocer estos
paquetes). Dado que el crecimiento económico se entiende como una mediada del
bienestar de la población, implícitamente se entiende que incide directamente
en la calidad de vida de las personas, por tanto, su estudio resulta relevante
en la elaboración de políticas.
1.
Trabajando los datos
(preliminar)
Antes
de poder trabajar los datos necesitamos organizarlos de forma que sean legibles
para R. Respecto a esta tarea, utilizamos el paquete readxl para cargar los datos,
posteriormente usamos el paquete tidyverse para seleccionar (select_if) solo aquellas columnas
establecidas en formato numérico o de carácter, lo que permite deshacernos de las
columnas en blanco en los Excel de CEPAL. Luego eliminamos las observaciones
que contiene datos perdidos, para deshacernos de los títulos y las leyendas de
las tablas (ojo, en caso de tener algún dato perdido, por ejemplo, el PIB
dominicano en 1990, esta observación se hubiese perdido, por lo que, el
procedimiento puede mejorarse).
library(tidyverse)
exceldata <-
readxl::read_excel('CrecCEPAL.xlsx',col_names = FALSE)
head(exceldata)
#
limpiando la base de datos
exceldata
<- exceldata %>%
select_if(function(col)
is.numeric(col) || is.character(col)) %>%
select(-2) %>%
drop_na()
colnames(exceldata)
<- as.character(exceldata[1,])
exceldata
<- exceldata[-1,]
Restructurando
la data: haciendo reshape
Para
facilitar el trabajo sobre la base de datos con el paquete tidyverse, se realiza un reshape utilizando la función melt. Esta organización de la base de
datos nos permitirá realizar operaciones rápidamente para cada país, sin
necesidad de utilizar bucles.
re_exceldata <- exceldata %>%
reshape2::melt(variable.name = "key",
value.names = "value",
id.vars = c("País")) %>%
arrange(País)
2.
Visualizar la evolución
del PIB
Una
vez contemos con nuestros datos organizados podemos realizar análisis por grupo
y representar la información contenida combinando el paquete dplyr con ggplot2. En el siguiente
ejemplo se muestra la evolución relativa del PIB, esta alternativa nos permite
estudiar el ritmo de crecimiento del producto de cada país, saltándonos las
diferencias de escala entre los países. Esta evolución relativa la creamos
dividiendo cada valor del PIB entre la primera observación disponible.
datastasas %>%
mutate(year =
as.Date(as.character(key), "%Y")) %>%
group_by(País)
%>%
mutate(IndicePIB = value/head(value,1))
%>%
ggplot( aes(x=year, y=IndicePIB,
colour=País)) +
geom_line() +
theme_minimal() +
theme(legend.position =
"none") +
scale_y_log10()
Note
que la mayoría de los países registraron crecimiento durante los 90’s aunque a
un ritmo heterogéneo y con importantes interrupciones regionales, como la de
México en 1994 y Brasil en 1998. Por lo que, esta década si bien se registra un
importante crecimiento económico mostró algunas sombras alrededor de la
capacidad de la región de mantener estable el crecimiento de la economía (Palazuelos, nd).
De
manera alternativa, para resaltar la evolución de un determinado país en un
contexto regional, podemos usar el paquete gghighlight para resaltar una serie
determinada, en este caso se muestra un ejemplo con la República Dominicana:
library(gghighlight)
datastasas %>%
mutate(year =
as.Date(as.character(key), "%Y")) %>%
group_by(País)
%>%
mutate(IndicePIB = value/head(value,1)) %>%
ggplot( aes(x=year, y=IndicePIB,
colour=País)) +
geom_line() +
theme_minimal() +
theme(legend.position =
"none") +
scale_y_log10() +
gghighlight(País
== "República Dominicana")
datastasas %>%
mutate(year =
as.Date(as.character(key), "%Y")) %>%
ggplot( aes(x=year, y=value)) +
geom_line(color="#00AFBB",
size=1) +
theme_minimal() +
stat_smooth(method =
"loess") +
facet_wrap(~País, scales =
"free")
3.
Promedio de crecimiento
por país
En
el siguiente ejemplo se realiza un análisis por grupo de países (group_by(País)) y se genera la variable
crecimiento (creci), que calcula la tasa
de crecimiento para cada país usando la función lag. Posterior, se usa el
comando summarise para obtener el
promedio de crecimiento de cada país, especificándole que existe una
observación na; se ordenan los datos
según el nivel de crecimiento y se indica que la variable país es un factor.
# Cacula el promedio de crecimiento por país y hace un llipograph
re_exceldata %>%
group_by(País)
%>%
mutate(value =
as.numeric(value),
creci = ((value/lag(value))-1)*100)
-> datastasas
# A tibble: 1,044 x 4
# Groups: País
[36]
País key
value creci
<chr> <fct>
<dbl> <dbl>
1 América
Latina 1990 6180. NA
2 América Latina 1991 6271.
1.47
3 América Latina 1992 6320.
0.767
4 América Latina 1993 6448.
2.03
5 América Latina 1994 6662.
3.33
6 América Latina 1995 6640. -0.337
7 América Latina 1996 6775.
2.04
8 América Latina 1997 7009.
3.45
9 América Latina 1998 7054.
0.650
10 América Latina 1999 6960. -1.34
# ... with 1,034 more rows
Posteriormente
se utiliza un lollipop
graph
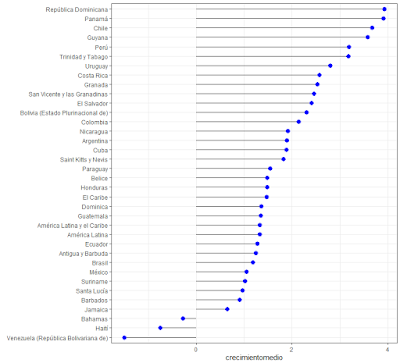
para representar el nivel promedio de crecimiento de cada país:
# Nivel promedio de crecimiento
datastasas %>%
summarise(crecimientomedio =
mean(creci, na.rm = T)) %>%
arrange(crecimientomedio)
%>%
mutate(País=factor(País,
levels=País)) %>%
ggplot( aes(x=País, y=crecimientomedio)) +
geom_segment(
aes(xend=País, yend=0)) +
geom_point(size=3, color="blue") +
coord_flip() +
theme_bw() +
xlab("")
El
gráfico verifica que la República Dominicana, Panamá y Chile corresponden a los
países de la región con mayor crecimiento entre 1990 y 2018, mientras que en el
extremo opuesto se encuentra Venezuela, Haití y Bahamas. Siendo el promedio de
crecimiento de la región igual a 1.33%, lo que indica que los países de la
región han crecido a ritmos bastantes disimiles durante el periodo. En el caso
dominicano, ha sido el segundo país de la región con mayor crecimiento de
productividad por mano de obra, solo detrás de Chile (Hofman, Mas, Aravena y Fernández, 2017, p.299). Este
evento se enmarca en términos históricos, en que las economías latinoamericanas
han crecido a expensa de sus exportaciones aunque dando paso al crecimiento
interno basado en el esquema ISI (Prebisch, nd). Posteriormente,
el crecimiento económico evidenciado en la región entre 1990 y 2010 se
considera relativamente bajo (Hofman, Mas, Aravena y Fernández, 2017).
Sin
embargo, los datos anteriores pudiesen estar incididos por observaciones
atípicas, por lo tanto, sería apropiado verificar la incidencia de estas y en
caso de ser significativa, proponer medidas robustas, como la mediana o la
media recortada. Para esto solo necesitaríamos modificar el estadístico
asignado a la variable crecimientomedio.
summarise(crecimientomedio = median(creci,
na.rm = T))
Otra
alternativa en el análisis del crecimiento podría ser analizar el crecimiento
medio por décadas (o periodos específicos), para esto podemos i) crear un
intervalo para cada década con la función cut, ii) quedarnos con los
dos primeros números de los años de la data o iii) utilizar la función cese_when. Usando esta última
función creamos la variable decada para identificar las
décadas y posteriormente hacemos un promedio de cada país por década (creci_de):
datastasas %>%
mutate(year =
as.numeric(as.character(key)),
decada
= case_when(year < 2000 ~
"90's",
year >= 2010 ~
"10's",
TRUE ~
"00's")
) %>%
group_by(País,decada) %>%
summarise(creci_de = mean(creci,na.rm =
T)) -> data_creci_De
data_creci_De
# A tibble: 108 x 3
# Groups: País [36]
País decada creci_de
<chr> <chr> <dbl>
1 América Latina 00's 1.65
2 América Latina 10's 0.952
3 América Latina 90's 1.34
4 América Latina y el Caribe
00's 1.66
5 América Latina y el Caribe
10's 0.941
6 América Latina y el Caribe
90's 1.34
7 Antigua y Barbuda 00's 1.73
8 Antigua y Barbuda 10's 0.764
9 Antigua y Barbuda 90's 1.17
10 Argentina
00's 1.49
# ... with 98 more rows
Aunque
una manera más elegante de presentar esta información es colocando el promedio
de crecimiento de cada década en distintas columnas, donde puede verificarse
más fácilmente que en la región hubo una importante desaceleración del
crecimiento durante la última década, incidida en parte a la incertidumbre
sobre la dinámica económica (CEPAL, 2019):
data_creci_De
%>%
mutate(decada = ordered(decada, levels =
c("90's","00's","10's"))) %>%
spread(key=decada, creci_de)
#
A tibble: 36 x 4
# Groups: País
[36]
País `90's`
`00's` `10's`
<chr> <dbl> <dbl>
<dbl>
1 América Latina 1.34 1.65
0.952
2 América Latina y el Caribe 1.34
1.66 0.941
3 Antigua y Barbuda 1.17 1.73
0.764
4 Argentina 3.48 1.49
0.751
5 Bahamas 0.798 -0.900 -0.677
6 Barbados 0.627 1.06
1.02
7 Belice 2.56 1.93
-0.0870
8 Bolivia (Estado Plurinacional
de) 1.87 1.83
3.27
9 Brasil 0.873 2.07
0.501
10 Chile
5.36 3.04 2.68
# ... with 26 more rows
Gráficamente
también podemos comparar el nivel promedio de crecimiento en la región en las
distintas décadas, en el siguiente ejemplo filtramos la primera y última
década, para poder verificar como cambia el crecimiento en los países (se
pudiera agregar el nombre de los países, pero por cuestión de estética de la presentación
no se hizo):
data_creci_De %>%
mutate(decada
= ordered(decada, levels =
c("90's","00's","10's"))) %>%
filter(decada
%in% c("90's","10's")) %>%
ggplot(aes(x=decada
, y=creci_de, group=factor(País))) +
geom_point(aes(colour=decada),
size=4.5, position=position_dodge(width=0.1)) +
geom_line(size=1, alpha=0.5, position=position_dodge(width=0.1)) +
xlab('Condition') +
ylab('Accuracy
(%)') +
scale_colour_manual(values=c("#009E73",
"#D55E00"), guide=FALSE) +
theme_minimal()
4.
Volatilidad del
crecimiento
Anteriormente
observamos el crecimiento medio en AL, sin embargo, la volatilidad ha sido un
fenómeno recurrente en la región, por lo que sería relevante estudiar su
evolución. En la figura siguiente se muestra un boxplot del crecimiento económico
para los países estudiados durante el periodo. Aunque hay que tener en cuenta
que la volatilidad está en función de las unidades de medición de las series,
siendo adecuado comparar los coeficientes de variación del crecimiento, como una
medida que normaliza esta volatilidad. Para verificar cual es el coeficiente de
variación para cada uno de los países usando summarise:
datastasas %>%
group_by(País)
%>%
summarise(coefVar = abs(sd(creci,na.rm = T)/mean(creci, na.rm = T)))
%>%
arrange(desc(coefVar))
# A tibble: 36 x 2
País coefVar
<chr> <dbl>
1 Bahamas 10.7
2 Venezuela (República Bolivariana
de) 5.65
3 Haití 5.44
4 Jamaica 5.41
5 Antigua y Barbuda 4.18
6 Suriname 3.77
7 Barbados 3.33
8 Cuba 3.20
9 Argentina 2.99
10 Santa Lucía
2.85
# ... with 26 more rows
Note
en el resultado anterior que los países de Bahamas, Venezuela y Haití son los
que mostraron mayor volatilidad del en el crecimiento durante el periodo.
Mientras que en el extremo opuesto se encuentra Bolivia, Salvador y República
Dominicana, como los países de la región con menor volatilidad del crecimiento.
Esta diferencia en el nivel e volatilidad indica que muchos países han estado
enfrentando incapacidad para garantizar el crecimiento económico en el largo
plazo (Palazuelos, nd).
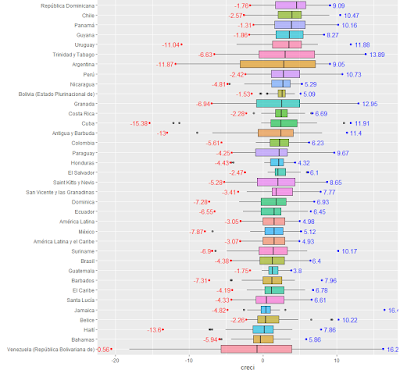
Un
ejemplo grafico de cómo obtener una visión general sobre el nivel mediano de
crecimiento y la dispersión de cada país se obtiene mediante un boxplot para cada país, resaltando los
valores extremos (máximo y mínimos) registrados en términos históricos:
datastasas %>%
mutate(País = factor(País)) %>%
ggplot(
aes(x=País, y=creci, fill=País)) +
geom_boxplot()
+
coord_flip() +
xlab("class") +
theme(legend.position="none")
+
xlab("") +
xlab("") +
stat_summary(geom = 'point', fun.y =
max, color="blue") +
stat_summary(geom = 'point', fun.y =
min, color="red") +
stat_summary(aes(label=round(..y..,2)), geom = 'text', fun.y = max,
color="blue", hjust = -0.25)+
stat_summary(aes(label=round(..y..,2)), geom = 'text', fun.y = min,
color="red", hjust = 1.1)
Lo
anterior, refleja una realidad altamente heterogénea en la región, tal como han
expuesto anteriormente Palazuelos (nd). Al verificar la
magnitud de la producción de los países, se verifican importantes diferencias
entre la incidencia de estados como México o Brasil, respecto a otras economías
más pequeñas de la región. Dado este enunciado, podríamos estar interesados en
organizar el boxplot anterior según la
mediana de crecimiento de los países (fct_reorder):
datastasas
%>%
ungroup() %>%
ggplot(
aes(x = fct_reorder(País, creci,
na.rm=T), y = creci, fill = País))+
geom_boxplot(alpha=.6) +
coord_flip() +
xlab("class") +
theme(legend.position="none") +
xlab("") +
xlab("") +
stat_summary(geom = 'point', fun.y = max, color="blue") +
stat_summary(geom = 'point', fun.y = min, color="red") +
stat_summary(aes(label=round(..y..,2)), geom = 'text', fun.y = max,
color="blue", hjust = -0.25)+
stat_summary(aes(label=round(..y..,2)), geom = 'text', fun.y = min,
color="red", hjust = 1.1)
Que
el nivel de crecimiento parezca estar asociado con la volatilidad del mismo,
nos puede llevar a estudiar la relación observada entre ambos fenómenos, esto
se realiza en el siguiente ejemplo con un gráfico de dispersión donde
relacionamos la volatilidad vs crecimiento. Primero creamos una base que
contenga las variables de interés agrupadas por país:
datastasas %>%
group_by(País)
%>%
summarise(PIBpc_last = last(value),
crecimmediano = mean(creci, na.rm = T),
coefVar = abs(sd(creci,na.rm = T)/mean(creci, na.rm = T)))
# A tibble: 36 x 4
País PIBpc_last
crecimmediano coefVar
<chr>
<dbl>
<dbl> <dbl>
1 América Latina 8881. 1.32
1.60
2 América Latina y el Caribe 8883. 1.33
1.59
3 Antigua y Barbuda 14141. 1.24
4.18
4 Argentina 10105. 1.89
2.99
5 Bahamas 26330. -0.283
10.7
6 Barbados 17762. 0.907
3.33
7 Belice 4224. 1.48
2.41
8 Bolivia (Estado Plurinacional
de) 2586. 2.30
0.635
9 Brasil 10905. 1.18
2.18
10 Chile 15443. 3.67
0.767
# ... with 26 more rows
Ahora
creamos un gráfico que relacione ambas variables, observándose una relación
negativa entre ambas variables, tal como plantearon Ramey y Ramey (1995):
datastasas %>%
group_by(País)
%>%
summarise(PIBpc_last = last(value),
crecimmediano =
median(creci, na.rm = T),
coefVar =
abs(sd(creci,na.rm = T)/mean(creci, na.rm = T))) %>%
ggplot(aes(x=coefVar,
y=crecimmediano, size=PIBpc_last)) +
geom_point() +
geom_smooth()+
theme_minimal() +
theme(legend.position="none") +
xlab("Volatilidad (Coef. Var.)") +
ylab("Crecimiento
(mediana)")
datastasas %>%
mutate(year =
as.numeric(as.character(key)),
decada
= case_when(year < 2000 ~
"90's",
year >= 2010 ~
"10's",
TRUE ~
"00's")
) %>%
group_by(País,decada) %>%
summarise(PIBpc_last = last(value),
crecimmediano =
median(creci, na.rm = T),
coefVar = abs(sd(creci,na.rm
= T)/mean(creci, na.rm = T))) %>%
ggplot(aes(x=coefVar,
y=crecimmediano, size=PIBpc_last)) +
geom_point() +
geom_smooth(method
= "lm")+
theme_minimal() +
theme(legend.position="none") +
xlab("Volatilidad
(Coef. Var.)") +
ylab("Crecimiento
(mediana)") +
scale_x_log10()
5.
Tendencia del producto
La
tendencia del producto suele ser una primera aproximación para el estudio de la
brecha del producto y la determinación el producto potencial. Usando El
análisis de la tendencia del PIB para la República Dominicana se puede
representar a partir de:
datastasas %>%
mutate(year =
as.Date(as.character(key), "%Y")) %>%
filter(País=="República
Dominicana") %>%
ggplot( aes(x=year, y=value)) +
geom_line(color="#00AFBB",
size=2) +
theme_minimal() +
stat_smooth(method = "loess")
6.
Brecha del producto para
cada país
La
brecha del producto de cada país se define a partir de la diferencia entre el
PIB potencial y el observado. Como el potencial es una variable latente, se
aproxima a partir de diversas estrategias, aquí se utiliza el filtro hp, disponible en R mediante la
función mFilter, para obtener la
tendencia del PIB. La brecha del producto de cada país en la región se presenta
en la siguiente matriz de gráficos de línea mediante el análisis group_by, sin necesidad de repetir la
operación para cada país:
datastasas %>%
group_by(País) %>%
mutate(trendPib =
unlist(mFilter::hpfilter(value,freq=12)["trend"]),
brecha
= value - trendPib,
year =
as.Date(as.character(key), "%Y"))
%>%
ggplot(aes(x=year,
y=brecha)) +
geom_line(color="#00AFBB",
size=1) +
theme_minimal() +
facet_wrap(~País, scales = "free")
7.
Ciclo del producto para
cada país
Para
llamar el ciclo solo necesitamos cambiar la indexación en el producto arrojado
por la función hpfilter:
datastasas %>%
group_by(País)
%>%
mutate(ciclo =
unlist(mFilter::hpfilter(value,freq=12)["cycle"]),
year =
as.Date(as.character(key), "%Y"))
%>%
ggplot(aes(x=year,
y=ciclo)) +
geom_line(color="#00AFBB",
size=1) +
theme_minimal() +
facet_wrap(~País, scales = "free")
Una
vez obtenido el ciclo económico de cada país, podemos cambiar la estructura de
la data (long) para que el ciclo de
cada país esté en una columna, y posteriormente obtener una matriz de
correlación para el análisis de la asociación del ciclo entre las naciones de
la región. Es importante notar que tanto en nivel como en volatilidad, así como
el ciclo económico, existen diferencias y similitudes entre las regiones lo que
dificulta las comparaciones entre países, cuestión planteada con anterioridad
en la literatura (Palazuelos, nd).
Lo
primero es hacer que el ciclo de cada región se encuentre en una columna y
luego utilizar el comando cor
para
poder obtener una matriz de correlación entre los ciclos económicos de la
región:
spread_c_data <- datastasas %>%
group_by(País)
%>%
mutate(ciclo =
unlist(mFilter::hpfilter(value,freq=12)["cycle"]),
year =
as.Date(as.character(key), "%Y"))
%>%
ungroup()
%>%
select(País,key,ciclo) %>%
spread(key=País,
ciclo)
# A tibble: 29 x 37
key `América Latina` `América Latina~ `Antigua y
Barb~ Argentina Bahamas Barbados Belice
<fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1990 16.9 18.0 -10.6 -235.
1384. 609. -175.
2 1991 2.23 2.93 19.5 -58.0
280. 212. -45.0
3 1992 -56.7 -56.5 -132. 126.
-757. -620. 151.
4 1993 -38.5 -39.3 84.3 120.
-916. -486. 216.
5 1994 66.1 64.4 430. 197.
-658. -169. 98.6
6 1995 -59.7 -59.3 -410. -332.
-364. -178. 6.92
7 1996 -20.7 -20.4 -110. -158.
-298. -4.24 -71.5
8 1997 130. 129. 61.7 303.
-156. 268. -109.
9 1998 113. 112. 162. 536.
-102. 456. -178.
10 1999 -26.3 -25.2 178. 242.
692. 225. -114.
spread_c_data[,-1]
%>%
cor()
En
caso de querer observar la relación de un país con la región se puede utilizar
la indexación:
spread_c_data[,-1] %>%
cor() %>%
.[,"República
Dominicana"] %>%
data.frame()
.
América
Latina 0.26144760
América
Latina y el Caribe 0.26670940
Antigua y Barbuda 0.55897088
Argentina 0.35427125