1.1. Experimento básico
La dificultad de obtener datos experimentales en cualquier
ciencia social dificulta observar efectos causales. Sin embargo, los diseños
experimentales intentan aproximar la obtención de efectos causales a partir de
datos observacionales, donde los factores muestran mayor variabilidad y menor
control respecto a cuándo el experimento se realiza en el contexto de un
laboratorio. En este marco, la variable resultado (o variable dependiente [y]) estaría siendo incidida por
variables independientes que se pueden observar (adicional a nuestra variable
de interés) y variables intervinientes no observadas, sobre la que debemos
establecer supuestos para poder alcanzar un “efecto causal”.
1.2. Análisis estadístico preliminar
En la presente entrada se muestran algunos ejemplos de
diseños experimentales utilizando R. De forma puntual se utiliza la data bwght del libro de
Econometría de J. Wooldridge, disponible en el paquete wooldridge. El siguiente
bloque de códigos adjunta la librería de ggplot2 para comparar el peso promedio de los niños al nacer (bwght) para dos grupos
especifico, segmentados según hayan o no fumado las madres durante el embarazo
(fuma). Note que es
importante definir la variable categórica como un factor. La función is.factor nos permite
verificar si una variable determinada está siendo considerada como un factor.
library(wooldridge)
library(ggplot2)
data(bwght)
attach(bwght)
bwght$fuma
<- factor(packs>0,
labels = c("No","Si"))
Es importante verificar el número de observaciones en cada categoría:
table(bwght$fuma)
No Si
1176 212
Un segundo antecedente es estudiar el peso promedio (o
mediano) por grupo puede obtenerse en R de distintas maneras, aquí mostramos
dos alternativas, la alternativa 1 está disponible en R (tapply) por default, la
segunda utiliza el paquete dplyr de tidyverse. Observándose que el peso mediano es superior entre las
mujeres que no fumaron durante el embarazo.
#Alt. 1
tapply(bwght$bwght,
bwght$fuma, median)
No Si
121 112
#Alt. 2
library(dplyr)
bwght %>%
group_by(fuma) %>%
summarise(median(bwght))
# A
tibble: 2 x 2
fuma
`median(bwght)`
<fct> <dbl>
1 No
121
2 Si
112
Además, una forma gráfica de obtener esta comparación es
mediante el grafico de caja o boxplot, el mismo, adicional a indicarnos la mediana de la serie,
nos permite ver la dispersión de la variable dependiente (bwght), lo que puede
darnos una idea de la significancia en la diferencia de media. Otra relevancia
del test es que permite verificar la presencia de valores atípicos.
ggplot(bwght,
aes(y=bwght, x=fuma)) +
geom_boxplot(outlier.colour="red")
+
theme_minimal()
Se puede observar que el peso promedio de los niños de madre
que no fuman durante el embarazo es ligeramente superior al resto, pero con una
amplia dispersión. En tal sentido, hay madres que fuman que tienen niños con un
peso superior al de madres que no fuman. Esta comparación de promedios pudiese
haber sido evidencia de un efecto causal en el marco de un experimento donde
los tratamientos se asignan aleatoriamente a las unidades experimentales (Maguiña,
2018), pero como los datos no son experimentales, es necesario establecer el
control de los factores observables (que estén disponibles en la base de datos)
y establecer supuestos sobre aquellos factores no observados, resumida en
aspectos como la equivalencia u homogeneidad entre los grupos. Es decir, no
podemos a este nivel, indicar que fumar es la razón de la diferencia entre grupos.
1.1. Prueba t de comparación de media
Un test formal de comparación de media es el test t de comparación
de media. Este test se realiza mediante el test t de comparación de media, que
se realiza en R con la función t.test cuya hipótesis nula es que no existen diferencia entre la
media de los grupos.
testt1
<- t.test(bwght$bwght~bwght$fuma,
alternative =
"two.sided",
var.equal = FALSE,
conf.level = 0.95)
testt1
Welch
Two Sample t-test
data: bwght$bwght by bwght$fuma
t =
6.1743, df = 302.29, p-value = 2.138e-09
alternative
hypothesis: true difference in means is not equal to 0
95
percent confidence interval:
6.073641 11.756355
sample
estimates:
mean in
group No mean in group Si
120.0612 111.1462
El p-valor obtenido claramente rechaza la hipótesis nula de
igualdad en media. Recordemos que el p-valor representa el área de la función de
densidad desde nuestro estadístico de prueba hasta el infinito, ahora, dado que
la diferencia entre el estadístico crítico y el de prueba es que nos permite
establecer una regla de rechazo de la nula, siempre rechazaremos la nula si el
p valor es menor al nivel de significancia seleccionado.
Los paquetes moonBook y webr nos permiten obtener una versión grafica (posiblemente más fácil
de interpretar) del test de hipótesis que hemos realizado anteriormente:
library(moonBook)
library(webr)
plot(testt1)
1.1. ¿Igualdad de la varianza?
Note que en el ejemplo anterior hemos supuesto varianzas
distintas (var.equal = FALSE), basados en el boxplot. Una prueba
formal que nos permite verificar si las varianzas son iguales es el test de
Bartlett, cuya hipótesis nula es que las varianzas son iguales. En R, esta
prueba se realiza mediante el comando bartlett.test:
library(car)
bartlett.test(bwght ~ nivelIng, data = bwght)
Bartlett
test of homogeneity of variances
data: bwght
by nivelIng
Bartlett's K-squared = 9.2027, df = 2, p-value =
0.01004
Adicionalmente, la prueba pwr pretende determinar el nivel de muestra necesario para alcanzar
un poder determinado, o calcular el poder, dado un tamaño de muestra. Según los
resultados, se necesitan muestra de al menos 83 individuos.
1.2. Test ANOVA
En el ejemplo, la mediana del peso de los niños cuyas madres
han fumado durante el embarazo, es notablemente inferior al resto. Sin embargo,
cuando necesitamos comparar más de dos grupos, como agregar el control de
factores externos se utiliza el test ANOVA.
El próximo ejemplo realiza una comparación de media del peso
al nacer entre tres grupos de ingresos. Para estos fines creamos la variable categórica
nivelIng que crea tres niveles de ingresos:
bwght$nivelIng
<- factor(cut(faminc, breaks = 3),
labels =
c("bajo","medio","alto"))
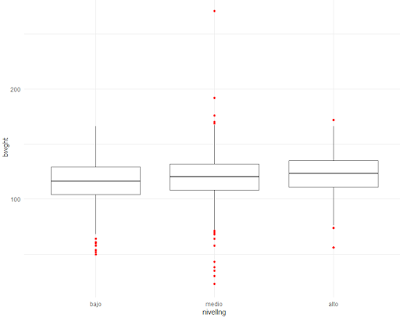
ggplot(bwght,
aes(y=bwght, x=nivelIng)) +
geom_boxplot(outlier.colour="red")
+
theme_minimal()
También podemos usar las maravillas del tidyverse, para comparar el
peso promedio de los niños al nacer para cada grupo de ingresos y observar que,
aun controlando por nivel de ingresos, continúan observándose diferencias
relativas en el peso de los niños según el consumo de cigarrillos de la madre.
Ahora bien, note la diferencia relativa, representada con la variable diffrel, se reduce en la medida
en aumentamos el nivel de ingresos del grupo, esto sería un indicador de los
factores externos no observados, tales como la educación o el acceso atenciones
médicas, estarían actuando en el problema.
bwght
%>%
group_by(nivelIng,fuma) %>%
summarise(medianas = median(bwght)) %>%
mutate(diffrel = (medianas/lag(medianas))-1)
# A tibble: 6 x 4
# Groups:
nivelIng [3]
nivelIng
fuma medianas diffrel
<fct> <fct> <dbl> <dbl>
1 bajo
No 119 NA
2 bajo
Si 110. -0.0714
3 medio
No 122 NA
4 medio
Si 114. -0.0697
5 alto No
124 NA
6 alto
Si 120. -0.0282
Primero mostramos un ejemplo de comparación de media cuando
tenemos varias categorías o clasificaciones, el test ANOVA (ANalysis Of VAriance),
basados en independencia, normalidad y homocedasaticidad, que permite comparar
distintos grupos (el test t visto anteriormente solo comparaba dos grupos).
Siendo la hipótesis nula, que no existen diferencias estadísticas entre las
medias de los grupos, el comando aov permite obtener la tabla Anova [referencia]:
anova_mod
<- aov(bwght ~ nivelIng, data = bwght)
summary(anova_mod)
Df Sum Sq Mean Sq F value Pr(>F)
nivelIng
2 8506 4253
10.4 3.27e-05 ***
Residuals
1385 566106 409
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
Claramente se rechaza la hipótesis nula de no diferencias
entre media.
1.1. Control de factores en el modelo ANOVA
Ahora, la mayor ventaja de esta metodología no es comparar
varios grupos, sino poder introducir el control explícito de variables como el
ingreso. El control de factores dentro de un modelo Anova se logra incluyendo
estas variables de forma explícita en los modelos. Este análisis es importante:
a. Cuando se necesita
estudiar el efecto de varios factores.
b. Para controlar el
resto de variables relevantes y que han sido observadas. Recuerde que es
necesario, como objetivo del diseño de la investigación, alcanzar que el
residuo del modelo sea aleatorio, por tanto, independiente de x.
Al realizar la comparación a lo interno de cada grupo de
ingresos, estamos introduciendo el control explícito del nivel de ingreso (a
menos que exista una alta dispersión a lo interno de cada grupo, de forma tal, que
aun controlando por grupos de ingreso la desigualdad a lo interno de estos
grupos pueda explicar diferencias importantes entro los individuos que lo
componen).
El siguiente ejemplo muestra como agregar factores en R:
anova_mod1
<- aov(bwght ~ fuma + faminc, data = bwght)
summary(anova_mod1)
Df Sum Sq Mean Sq F value Pr(>F)
fuma
1 14276 14276
35.527 3.19e-09 ***
faminc
1 3803 3803
9.464 0.00214 **
Residuals
1385 556533 402
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
1.2. Validar el modelo ANOVA
1.2.1.
Testear autocorrelación
La validez del modelo Anova depende fundamentalmente de que
los residuos asuman un comportamiento aleatorio y normal. El Box-Pierce test
testea independencia lineal (autocorrelación) entre las observaciones (una
alternativa grafica se obtiene con los correlogramas acf(re)).
re
<- anova_mod$residuals
Box.test(re)
Box-Pierce
test
data: re
X-squared
= 2.58, df = 1, p-value = 0.1082
En el ejemplo anterior no es posible rechazar la hipótesis
nula. Note, que en caso de que se rechace la hipótesis de no autocorrelación a
un nivel del 5%, lo que indicaría cierta estructura de autocorrelación en los
residuos. Esto podría ser resultado de alguna variable omitida, debido a que
esta versión se corresponde con la del modelo de regresión simple. En términos
llanos, esto indica que necesitaríamos intentar incluir nuevos modelos o
modificar la forma funcional del modelo, para intentar no rechazar la nula.
1.2.2.
Testear normalidad
El gráfico qq-plot permite comparar la distribución empírica de nuestros datos,
con aquella esperada en caso de que nuestra variable se distribuya como una
normal. Usando el paquete tidyverse este se obtiene como:
ggplot(data.frame(re),
aes(sample = re)) +
stat_qq() +
stat_qq_line() +
theme_minimal()
Sin embargo, en muchos casos los test gráficos pueden no ser
concluyentes. Para esto se usa el test shapiro.test, cuya hipótesis nula es que la variable de interés se
comporta como una normal:
shapiro.test(re)
Shapiro-Wilk normality test
data: re
W =
0.97459, p-value = 6.276e-15
Cuando no se cumple con los supuestos de base, es
recomendable usar un test no paramétrico.
kruskal.test(bwght$bwght~bwght$fuma)
Kruskal-Wallis rank sum test
data:
bwght$bwght by bwght$fuma
Kruskal-Wallis chi-squared = 38.987, df = 1,
p-value = 4.267e-10
1.1. Test de Tukey
Hasta aquí hemos usado un test paramétrico ANOVA para
comparar media entre grupos, pero este no aporta información sobre las
diferencias especificas entre los grupos. El test crea intervalos de confianzas
y compara las distintas clases, para contrastar diferencias en media entre
estas. De esta forma, podemos identificar a cuáles grupos específicos responden
las posibles diferencias en media identificadas por el test Anova.
testtukey
<- TukeyHSD(anova_mod)
testtukey
Tukey
multiple comparisons of means
95% family-wise confidence
level
Fit:
aov(formula = bwght ~ nivelIng, data = bwght)
$nivelIng
diff lwr upr
p adj
medio-bajo 3.912042 1.0809266
6.743158 0.0034789
alto-bajo
6.551258 2.9552061 10.147309
0.0000608
alto-medio 2.639215 -0.8809485 6.159379 0.1839291
El test anterior indica que no existen diferencia en el peso medio en los bebes de los grupos alto-medio, contrario a los demás grupos comparados, donde si se observan diferencias. Podemos graficar estos resultados utilizando la función plot. Esta prueba gráfica utiliza la lógica de un intervalo de confianza, si el cero está contenido en el intervalo de confianza, no podemos rechazar la nula de que esta diferencia sea igual a cero.
plot(testtukey)
1.1. Anova factor
El factor permite estimar diversas combinaciones de un grupo
de variables. La forma funcional de esta especificación incluye interacciones entre
estás.
anova_mod2
<- aov(bwght ~ fuma * male * white, data = bwght)
summary(anova_mod2)
Df Sum Sq Mean Sq F value Pr(>F)
fuma
1 14276 14276
36.015 2.50e-09 ***
male
1 2481 2481
6.259 0.0125 *
white 1 9333
9333 23.545 1.36e-06 ***
fuma:male 1
544 544 1.372
0.2417
fuma:white 1
507 507 1.280
0.2582
male:white 1
36 36 0.090
0.7644
fuma:male:white 1
425 425 1.072
0.3006
Residuals
1380 547011 396
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
En este caso, los estadísticos de prueba son distintos. Note que
una vez controlada la raza y el sexo del niño, no se observan diferencias
significativas en la media del peso de los niños. Ahora bien, los estadísticos de
prueba ahora son distintos, estos se obtienen mediante:
drop1(anova_mod2,
~., test="F")
Single
term deletions
Model:
bwght ~
fuma * male * white
Df Sum of Sq RSS
AIC F value Pr(>F)
<none> 547011 8311.5
fuma 1 16.3 547027 8309.6 0.0412 0.8392641
male 1
1479.6 548490 8313.3 3.7327
0.0535627 .
white 1
5763.7 552774 8324.1 14.5406 0.0001432 ***
fuma:male 1
863.4 547874 8311.7 2.1781
0.1402158
fuma:white 1
941.5 547952 8311.9 2.3752
0.1235033
male:white 1
186.2 547197 8310.0 0.4699
0.4931618
fuma:male:white 1
425.0 547436 8310.6 1.0722
0.3006339
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
Referencias
-
Calvo, J.; Polazón, F.; Carreño, P. (2016). Diseño
experimental y análisis estadístico. Universidad de Murcia. Consultado
27/2/2020. Disponible en: https://aulavirtual.um.es/access/content/group/COLLAB-x5vsnmqzqac8cs9edm6rhxm/DISE%C3%91O%20EXPERIMENTAL%20Y%20AN%C3%81LISIS%20DE%20DATOS/DEyAE%20guion.pdf
-
Maguiña, M. (2018). Introducción
a los diseños experimentales. Consultado 27/2/2020. Disponible en: https://rpubs.com/misael892/DCAyBCA.
-
Mendiburu, F. (2007). Diseño
y Análisis de experimentos Aplicados en investigación Agrícola.