La
siguiente entrada introduce el uso de funciones de correlación en R u su análisis, usando la
data iris disponible en el programa. Tenga en cuenta que como los datos usualmente no provinenen de experimentos, la correlación es una medida de asociación entre el movimiento de dos variables, no de causalidad:
> attach(iris)
> head(iris)
Sepal.Length
Sepal.Width Petal.Length Petal.Width Species
1 5.1
3.5 1.4 0.2
setosa
2 4.9
3.0 1.4 0.2
setosa
3 4.7
3.2 1.3 0.2
setosa
4 4.6
3.1 1.5 0.2
setosa
5 5.0
3.6 1.4 0.2
setosa
6 5.4
3.9 1.7 0.4
setosa
Una
primera forma de visualizar la relación entre dos variables (para estudiar su relación) cuando una es cuantitativa
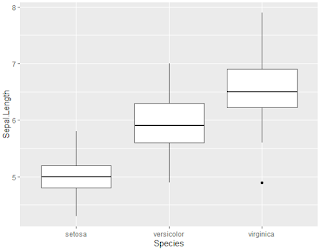
y otra cualitativa, es por medio de la comparación de media. La misma, intenta verificar si el promedio condicional (E[y|c]) es igual al promedio
incondicional (E[y]), en caso correcto, de que el promedio en los diversos
grupos sea el mismo, se establece independencia, en caso contrario no. Usando
ggplot2 generamos un boxplot para cada especie de la variable Sepal.Length:
> library(ggplot2)
ggplot(data = iris, aes(y = Sepal.Length , x =
Species)) +
geom_boxplot()
En
el caso de querer comparar dos variables continuas, el proceso es
discrezionalizar una de esas variables segmentándola en grupos para posteriormente obtener la media para cada grupo. Este proceso se realiza en R mediante la función cut:
ggplot(data = iris,
aes(x =
cut(Sepal.Length , breaks = 3), y = Sepal.Length)) +
geom_boxplot()
1.1.
Covarianza y correlación
Una
primera medida de asociación lineal entre dos variables cuantitativas resulta
de la covarianza entre ellas. Dado que la covarianza es una esperanza del
producto de dispersiones de las variables en torno a su media, esta indicaría
donde en promedio tiende a estar una de las variables cunado la otra está por
encima o por debajo de su media:
> dsepall <- Sepal.Length – mena(Sepal.Length)
> dsepalw <- Sepal.Width – mean(Sepal.Width)
>
> ggplot(data.frame(dsepall,dsepalw),
aes(x=dsepall, y=dsepalw)) +
+ geom_point()
+
+
geom_hline(yintercept=0, linetype="dashed", color =
"red") +
+
geom_vline(xintercept=0, linetype="dashed", color =
"red") +
+ theme_minimal()
La
matriz de varianza covarianza de una matriz cuadrada y simétrica, que recoge
información sobre las covarianzas de las series (fuera de su diagonal
principal) y la varianza de estas (en su diagonal principal). Esta matriz de varianzas covarianzas se
obtiene en R mediante la función var.
> dataM <- cbind(Sepal.Length, Sepal.Width)
> var(dataM)
Sepal.Length Sepal.Width
Sepal.Length 0.6856935
-0.0424340
Sepal.Width -0.0424340
0.1899794
Pero
como la covarianza está asociada con la escala de las series, esta solo informa
de la dirección de la relación, no así de la magnitud, por tanto, para obtener
una medida normalizada de esta relación se utiliza el coeficiente de correlación que toma valores entre -1 y 1, según la
dirección de la relación lineal entre las variables. Acercándose a los extremos
(|1|) en caso de mayor asociación lineal entre las variables. Por tanto, la
correlación es una medida normalizada de la relación entre dos variables
cuantitativas continuas (Vinuesa, 2016). La matriz de correlación en R se obtiene a partir de cor.
> mcor<-round(cor(dataM),2)
> mcor
Sepal.Length Sepal.Width
Sepal.Length 1.00 -0.12
Sepal.Width -0.12 1.00
Use
?cor en su consola para
verificar diversas opciones, como use
= "complete.obs",
que permite indicarle cuales observaciones se usaran para calcular el coeficiente.
Alternativamente
usando el paquete dplyr:
>
iris %>%
+
summarize(N = n(), r =
cor(Sepal.Length, Sepal.Width))
N
r
1
150 -0.1175698
Dado
que la matriz es simétrica, podemos representarla con valores nulos en su
triangular superior o inferior, según el deseo del analista:
> mcor[upper.tri(mcor)]<-""
> as.data.frame(mcor)
Sepal.Length Sepal.Width
Sepal.Length
1
Sepal.Width -0.12 1
Una
medida gráfica para estudiar la relación entre variables se obtiene con el gráfico de dispersión. Este gráfico
permite: i) ver forma de la relación; ii) atípicos; iii) dirección y fuerza de
la relación; iv) variabilidad (Ferrero y Lopéz, 2019).
ggplot(iris, aes(x=Sepal.Length, y=Sepal.Width)) +
geom_point()
+
geom_smooth(method=lm) +
theme_minimal()
Ojo: Tenga pendiente que el
coeficiente de correlación de Pearson es igual a corr(x,y)=cov(x,y)/ds(x)ds(y), por lo qué,
transformaciones de variables que lleven a incrementar disminuir la varianza, como el logáritmo, moverá la
correlación (a continuación colocamos un brece ejemplo). En
el caso de series de tiempo tenga pendiente que las series usadas para calcular
la correlación debe ser estacionaria para evitar obtener relaciones falsas. Además, tener cuidado con el efecto que
tienen ciertas técnicas de imputación sobre la varianza, dado que modificarían
el coeficiente de correlación entre estas:
>
x<-c(1:4)
>
y1<-c(1,3,5,9)
>
y2<-c(1,3,6,10)
>
>
data.frame(desStan = c(sd(y1), sd(y2)),
+ Correla = c(cor(x,y), cor(x,y))
+ )
desStan
Correla
1
3.41565 0.9890707
2
3.91578 0.9890707
Continuando
con la función cor de R, modificando el
argumento "method" podemos obtener
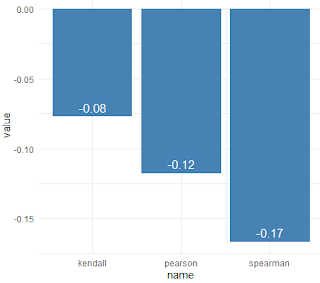
diversas versiones del coeficiente de correlación, siendo el coeficiente de Pearson
el más comúnmente usado. Verifique que los valores asociados a queda coeficiente
difieren de manera importante:
> per <- cor(Sepal.Length, Sepal.Width, method =
"pearson")
> ken <- cor(Sepal.Length, Sepal.Width, method =
"kendall")
> spe <- cor(Sepal.Length, Sepal.Width, method =
"spearman")
>
> # Create data
> data <- data.frame(
+
name=c("pearson","kendall","spearman")
,
+
value=c(per,ken,spe)
+ )
> data
name value
1 pearson
-0.11756978
2 kendall
-0.07699679
3 spearman -0.16677766
> # Barplot
> ggplot(data, aes(x=name, y=value)) +
+
geom_bar(stat = "identity", fill="steelblue") +
+
geom_text(aes(label=round(value,2)),
+
vjust=-0.5,
+
color="white",
+
size=4.5) +
+
theme_minimal()
Para
decidir cuál es el método que se requiere usar necesitamos verificar el
supuesto de normalidad e independencia en la serie estudiada, dado que estos
supuestos son asumidos por el coeficiente de Pearson. Speraman representa una
alternativa no paramétrica en caso de no verificarse los supuestos. El test de
normalidad en R está disponible con la función shapiro.test, siendo h0=normalidad.
> shapiro.test(Sepal.Length)
Shapiro-Wilk
normality test
data:
Sepal.Length
W = 0.97609, p-value = 0.01018
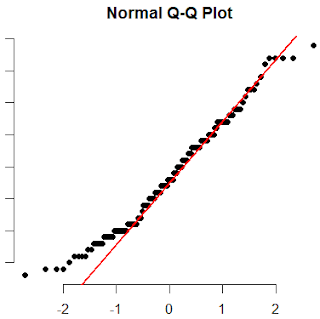
Un
test gráfico (qq-plot):
> qqnorm(Sepal.Length, pch = 16, frame = FALSE)
> qqline(Sepal.Length, col = "red", lwd =
2)
1.1.
Análisis condicional
Usualmente,
es necesario verificar la correlación para grupos específicos de mis datos,
dado que esta correlación global observada hasta aquí puede variar de forma
importante a lo interno de dichos grupos. Las siguientes dos alternativas
muestran como obtener el coeficiente para grupos determinados de mis datos. En
la primera alternativa (1) se utiliza indexación lógica para obtener los valores de las variables (x[]) que corresponden a la Specie setosa
(Species=="setosa"). Mientras que la segunda alternativa utiliza la misma
lógica, con la salvedad que el filtro se realiza para la base completa y no
únicamente para las variables de interés.
> # Alt 1: indexación de las variables
> cor(Sepal.Length[Species=="setosa"],
Sepal.Width[Species=="setosa"])
[1] 0.7425467
> # Alt 2: crear la data filtrada anterior
> data1 <- iris[Species=="setosa",]
> cor(data1$Sepal.Length, data1$Sepal.Width)
[1]
0.7425467
En
el caso de buscar la correlación para todos los grupos de variables de forma
simultánea, podemos usar el comando by, este permite obtener
la matriz de correlación para cada uno de los grupos. Note, como se modifican
los coeficientes cuando se realiza el análisis condicional:
> by(iris[,1:2], Species, cor)
Species: setosa
jojo1 Sepal.Width
jojo1 1.0000000 0.7425467
Sepal.Width 0.7425467 1.0000000
---------------------------------------------------------------------
Species: versicolor
jojo1 Sepal.Width
jojo1 1.0000000 0.5259107
Sepal.Width 0.5259107 1.0000000
---------------------------------------------------------------------
Species: virginica
jojo1 Sepal.Width
jojo1 1.0000000 0.4572278
Sepal.Width 0.4572278 1.0000000
Para
obtener únicamente los coeficientes de correlación entre las variables, podemos
utilizar la función vectorizada (este tipo de funciones evitan utilizar loops
al repetir un procedimiento determinado para cada uno de los sub-grupos
indicados) lapply (la función unlist ayuda a obtener este resultado como un vector, no como lista):
> lapply(split(iris, Species),
function(x){cor(x[,1], x[,2])})
$setosa
[1] 0.7425467
$versicolor
[1] 0.5259107
$virginica
[1] 0.4572278
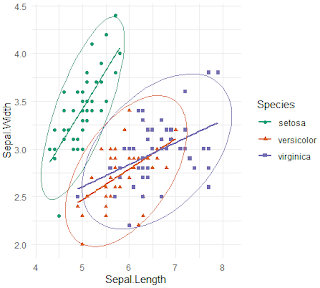
> ggplot(iris, aes(x=Sepal.Length, y=Sepal.Width,
shape=Species, color=Species)) +
+ geom_point()
+
+
geom_smooth(method=lm, se=F, fullrange=F)+
+
scale_color_brewer(palette="Dark2")+
+
theme_minimal() +
+
stat_ellipse(type = "norm")
Una
alternativa para visualizar la relación entre variables en las diversas
especies:
> ggplot(data = iris, aes(x = Sepal.Length, y = Sepal.Width)) +
+ geom_point() +
+ facet_wrap(~ Species)
Para
aplicar las diversas metodologías de estimación del coeficiente de correlación
al grupo de variables,
by(iris[,1:2],
Species, function(x) cor(x, method =
"spearman"))
Species: setosa
jojo1 Sepal.Width
jojo1 1.0000000 0.7553375
Sepal.Width 0.7553375 1.0000000
---------------------------------------------------------------------
Species: versicolor
jojo1 Sepal.Width
jojo1 1.000000 0.517606
Sepal.Width 0.517606 1.000000
---------------------------------------------------------------------
Species: virginica
jojo1 Sepal.Width
jojo1 1.0000000 0.4265165
Sepal.Width 0.4265165
1.0000000
Alternativa
usando dplyr:
> iris %>%
+ group_by(Species) %>%
+ summarize(N = n(), r =
cor(Sepal.Length, Sepal.Width))
# A tibble: 3 x 3
Species N
r
<fct> <int> <dbl>
1 setosa 50 0.743
2 versicolor 50 0.526
3 virginica 50 0.457
1.1. Test
Finalmente,
podemos estar interesados en conocer la significancia del coeficiente de
correlación identificado. El estadístico t asociado al test a la hipótesis nula
de que g0: rho=0:
> t_cor
<- (per/sqrt(1-per^2))*sqrt(length(Sepal.Length)-2)
>
> pvalor
<- 2*pt(t_cor, (length(Sepal.Length)-2), lower.tail = T)
>
> c(trho = t_cor, df=length(Sepal.Length)-2, p.valor=pvalor)
trho df
p.valor
-1.4402871 148.0000000 0.1518983
Para
realizar el contraste directamente en R, se puede testear mediante la función cor.test:
> cor.test(Sepal.Length, Sepal.Width, method =
"pearson")
Pearson's
product-moment correlation
data:
Sepal.Length and Sepal.Width
t = -1.4403, df = 148, p-value = 0.1519
alternative hypothesis: true correlation is not equal
to 0
95 percent confidence interval:
-0.27269325
0.04351158
sample estimates:
cor
-0.1175698
El
paquete Hmisc permite visualizar
conjuntamente los coeficientes y los valores p a partir de dos matrices, una
con los crecientes de correlación y una segunda matriz con los valores p.
>
rcorr(as.matrix(iris[,-5]))
jojo1 Sepal.Width Petal.Length
Petal.Width
Sepal.Length 1.00 -0.12 0.87 0.82
Sepal.Width -0.12 1.00 -0.43 -0.37
Petal.Length 0.87 -0.43 1.00 0.96
Petal.Width 0.82 -0.37 0.96 1.00
n= 150
P
jojo1 Sepal.Width Petal.Length Petal.Width
Sepal.Length 0.1519 0.0000 0.0000
Sepal.Width 0.1519 0.0000 0.0000
Petal.Length 0.0000 0.0000 0.0000
Petal.Width 0.0000 0.0000 0.0000
Referencias:
-
Baumer,
Benn (2017). Correlation and regression in R. Data.Camp.
-
Ferrero, R.; Lopéz, J. (2019). Análisis de correlación: guía rápida en R. Consultado 1/2/2020.
Disponible en: https://www.maximaformacion.es/blog-dat/analisis-de-correlacion-en-r/.
-
Grothendieck, G.
(2006). Correlations by group. Consultado 1/2/2020. Disponible en: https://stat.ethz.ch/pipermail/r-help/2006-July/109859.html.
-
Sthda.com
(nd). Correlation Test Between Two
Variables in R. Consultado 1/2/2020. Disponible en: http://www.sthda.com/english/wiki/correlation-test-between-two-variables-in-r.
-
Vinuesa, P. (2016). Tema 8 - Correlación: teoría y práctica.
Consultado 1/2/2020. Disponible en: https://www.ccg.unam.mx/~vinuesa/R4biosciences/docs/Tema8_correlacion.html.