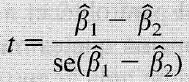En esta primera parte estimamos
el modelo de regresión que servirá de ejemplo, utilizando la base
"wage1", disponible en el libro de econometría de Wooldridge. El
modelo de prueba es el siguiente:
wage ~ educ +
exper + expersq + female + services
A continuación, se muestra como estimar este modelo de regresión lineal en R:
>
library(wooldridge))
> attach(wage1)
> str(wage1)
'data.frame': 526 obs. of 24 variables:
$
wage : num 3.1 3.24 3 6 5.3 ...
$
educ : int 11 12 11 8 12 16 18 12 12 17 ...
$
exper : int 2 22 2 44 7 9 15 5 26 22 ...
$
tenure : int 0 2 0 28 2 8 7 3 4 21 ...
$
nonwhite: int 0 0 0 0 0 0 0 0 0 0 ...
$
female : int 1 1 0 0 0 0 0 1 1 0 ...
$
married : int 0 1 0 1 1 1 0 0 0 1 ...
$
numdep : int 2 3 2 0 1 0 0 0 2 0 ...
$
smsa : int 1 1 0 1 0 1 1 1 1 1 ...
$
northcen: int 0 0 0 0 0 0 0 0 0 0 ...
...
>
modeloPUCMM<-lm(wage~educ+exper+expersq+female+services, data=wage1)
>
#options(scipen=999)
>
summary(modeloPUCMM)
Call:
lm(formula
= wage ~ educ + exper + expersq + female + services,
data = wage1)
Residuals:
Min 1Q Median 3Q
Max
-6.8714
-1.8251 -0.4038 1.1991 14.1943
Coefficients:
Estimate Std. Error t value
Pr(>|t|)
(Intercept)
-2.1761619 0.7381443 -2.948 0.00334 **
educ
0.5506381 0.0501278 10.985 <
2e-16 ***
exper
0.2539042 0.0347204 7.313 9.95e-13 ***
expersq
-0.0043956 0.0007731 -5.686 2.17e-08 ***
female
-2.0495114 0.2628519 -7.797 3.48e-14 ***
services
-1.0225149 0.4348036 -2.352 0.01906 *
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.976 on 520
degrees of freedom
Multiple
R-squared: 0.357, Adjusted
R-squared: 0.3508
F-statistic:
57.73 on 5 and 520 DF, p-value: < 2.2e-16
Aquí suponemos el modelo es el
correcto, pero en un ejercicio real, deben verificarse el cumplimiento de los
supuesto correspondientes (como no heterocedasticidad) antes de realizar las
pruebas.
1.1. Test de significancia individual: a partir de un estadístico
de prueba (t)
Lo importante siempre es
identificar nuestra hipótesis nula y nuestra hipótesis alternativa, a un nivel
de significancia dada. Porque estos elementos definirán la forma de nuestro
test. Referidos al test de significancia individual, nuestra hipótesis nula es
que nuestro coeficiente es igual a cero, en otras palabras, testea la
independencia entre ambas variables (x,y), dado que este coeficiente recoge la pendiente estimada
de la relación entre una variable dependiente (x) y la esperanza condicional de y a los
valores de x (E[y|x]), por lo
que, un valor de cero indicaría que esta esperanza es la misma
independientemente al valor asumido por x (independencia).
Ho: beduc = 0
Ha: beduc no es igual a
0
Nivel de confianza = 95%
Ahora, sabiendo el tipo de distribución retórica de mi estadístico
de prueba, necesitamos obtener el t teórico o t de tabla (tt) dados unos grados
de libertad y nuestro t calculado, que resulta de la estimación alcanzada.
Sobre ambos valores se establece la regla de rechazo de la hipótesis nula.
>
# Ejemplo: Testear la significancia individual de educ mediante el test de
significancia
>
# Método: Estadístico de prueba
> # Paso 1: Construir el t
calculado, necesario para estimar tc=b_estimado/ee(b_estimado)
> # Puedo recuperar directamente
mis coeficientes de los modelos
>
coef(modeloPUCMM)[2]
educ
0.5506381
> # Alternativa 1
>
beduc<-coef(modeloPUCMM)["educ"]
> # Alternativa 2
>
coef(modeloPUCMM)[[2]]
[1]
0.5506381
> # Desviación estándar del
coeficiente: llamándolo de mi matriz de varianzas covarianzas
>
mvc <- vcov(modeloPUCMM)
>
dsbeta1<-sqrt(mvc[2,2])
> dsbeta1
[1] 0.05012778
> # t calculado
>
tc<-beduc/dsbeta1
>
tc
educ
10.98469
> # T tabla
>
glb <- length(wage)-length(coef(modeloPUCMM))
>
glb <- df.residual(modeloPUCMM) #alternativa
> alpha<-0.05
>
tt <- qt(1-alpha/2, glb)
> # Recordad que rechazamos la
hipótesis nula si: abs(tc)>abs(tt)
>
# Regla de rechazo bo=beta_educ=0
>
paste("Rechazamos H0?", abs(tc)>abs(tt))
[1]
"Rechazamos H0? TRUE"
Observe que estos son los
resultados que el programa arroja por default. Es decir, que podemos
interpretarlos de forma directa en la salida del programa. Claramente, dada la
regla de rechazo (abs(tc)>abs(tt)), rechazamos la hipótesis nula.
educ
0.5506381 0.0501278 10.985 < 2e-16 ***
1.2. Test de significancia individual: a partir
del p-valor
Ahora testeamos la misma
hipótesis nula del ejercicio anterior, pero utilizando el p-valor como método
de decisión. En este caso, la regla de rechazo se establece alrededor del nivel
de significancia, rechazamos la hipótesis en caso de que el p-valor sea
inferior al nivel crítico elegido. Para ver esto más directamente, recordemos
que el p.valor es una suma del área bajo la curva de densidad que esta entre el
t calculado y el +inf, por lo que, esta solo será inferior al nivel crítico
cuando el t.calculado sea inferior al t.tabla (teórico). Vea que un p.valor de
cero (<0.05), nos lleva a rechaza la hipótesis nula.
>
#pt distribution function
>
p.valor <- 2*(1-pt(abs(tc), glb))
>
p.valor
educ
0
1.3. Test de significancia individual: a partir del Intervalo de
confianza
Finalmente, utilizamos el
método del intervalo de confianza para crear un rango alrededor del coeficiente
estimado, y es alrededor de este rango donde rechazamos o no nuestra hipótesis
nula. Cuando el valor testeado se encuentra dentro de este rango, no rechazamos
nuestra hipótesis nula, en caso contrario, sí.
>
lowb <- beduc-tt *dsbeta1 # lower bound
>
upb <- beduc+tt *dsbeta1 # upper bound
>
c(beduc, lowb, upb)
educ educ educ
0.5506381
0.4521603 0.6491160
Existen alternativas para obtener
intervalos de confianza a distintos niveles, para cada uno de nuestros
coeficientes. Lo que nos permite testear una cantidad infinita de valores de
parámetros, sin necesidad de modificar nuestros resultados. Es decir, podemos
testear cualquier valor del coeficiente asociado a educación, sin necesidad de
re-calcular nada. La regla de
rechazo es ahora, rechazo toda hipótesis nula cuyo valor quede excluido del
intervalo de confianza construido.
>
confint(modeloPUCMM , level = 1-alpha)
2.5 %
97.5 %
(Intercept)
-3.626273351 -0.726050391
educ
0.452160261 0.649115974
exper
0.185694681 0.322113621
expersq
-0.005914339 -0.002876928
female
-2.565893655 -1.533129192
services
-1.876702420 -0.168327374
>
confint(modeloPUCMM , level = 1-alpha)["educ",]
2.5 %
97.5 %
0.4521603
0.6491160
> # testear si beduc = 0
>
# Regla de rechazo bo=beta_educ=0
>
paste("Rechazamos H0?", 0<lowb & upb>0)
[1]
"Rechazamos H0? TRUE"
2. Test t para valores específicos de nuestros coeficientes
Ahora, utilizando el mismo
procedimiento anterior, podemos testear si cualquier coeficiente asume un valor
determinado. En el siguiente ejemplo verificamos mediante un estadístico de
prueba, si el parámetro poblacional puede ser igual a 0.5. La dinámica es
justamente igual, siempre que la hipótesis sea de dos colas y al mismo nivel de
significancia, solo necesitamos modificar el estadístico de prueba o t
calculado.
Ho: beduc = 0.5
Ha: beduc no es igual a
0.5
Nivel de confianza = 95%
> h0 <- a <- 0.5
>
alpha <- 0.05
>
tc1 <- (beduc-h0)/dsbeta1
>
tc1
educ
1.010181
> tt
[1]
1.964537
> paste("Rechazamos
H0?",abs(tc1)>abs(tt))
[1]
"Rechazamos H0? FALSE"
Ahora, repetimos la prueba anterior,
pero modificando el nivel de confianza al 90%.
>
# ho: betaeduc = 0.5
>
# ha: betaeduc no es igual a 0.5
>
# al 90% de nivel de significancia
> alpha1 <- 0.1
>
tt1 <- qt(1-alpha/2, glb)
>
tt1
[1]
1.964537
> paste("Rechazamos
H0?",abs(tc1)>abs(tt))
[1]
"Rechazamos H0? FALSE"
Observe que, en caso de modificar el tipo de prueba a una sola
cola, solo necesitamos quitar la división entre dos, al estimar el estadístico de
prueba. Recordemos que este estadístico corresponde a un percentil teórico.
1-alpha/2 #Dos colas
1-alpha/2 #1 cola
3. Test t para combinación lineal de parámetros
3.1. Test t
En el primer ejemplo de esta parte, comparamos si los coeficientes
asociados a educación y experiencia son iguales ( h0: beduc == bexper).
>
# Test de combinación de parámetros
>
# h0: beduc == bexper
>
# h0: beduc no son iguales bexper
>
# alpha = 5%
>
beduc<-coef(modeloPUCMM)["educ"]
>
bexper<-coef(modeloPUCMM)["exper"]
Note que ahora el t.calculado
requiere el uso de la matriz de varianzas-covarianzas de los coeficiente para
calcular la V(b1+b2) de los coeficientes (ver la propiedades de la
varianza).
>
# t calculado
>
tc3<-(beduc-bexper)/sqrt(mvc[2,2]+mvc[3,3]-2*mvc[2,3])
>
mvc["educ","educ"]==mvc[2,2] #Alternativa para llamar
la varianza
[1]
TRUE
> #t tabla
>
# Cuando modificamos el nivel significancia de la prueba, se modifica
alpha
>
alpha<-0.05
>
tt3 <- qt(1-alpha/2, glb)
> # Regla de rechazo
beduc == bexper
>
paste("Rechazamos H0?",abs(tc3)>abs(tt))
[1]
"Rechazamos H0? TRUE"
3.2. Contraste de combinaciones
lineales (test F)
La función linearHypothesis
(del paquete car) ofrece una alternativa a testear esta hipótesis usando un
estadístico F.
>
# Alternativa
>
library(car)
>
linearHypothesis(modeloPUCMM, c("educ - exper=0"))
Linear
hypothesis test
Hypothesis:
educ
- exper = 0
Model 1: restricted model
Model
2: wage ~ educ + exper + expersq + female + services
Res.Df RSS Df Sum
of Sq F Pr(>F)
1
521 4801.9
2
520 4604.5 1 197.44 22.298 3.007e-06 ***
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Esta alternativa es
verificar si beduc = 2*bexper.
>
# Testear H0: beduc = 2*bexper
>
linearHypothesis(modeloPUCMM, c("educ - 2*exper=0"),
test="F")
Linear
hypothesis test
Hypothesis:
educ
- 2 exper = 0
Model 1: restricted model
Model
2: wage ~ educ + exper + expersq + female + services
Res.Df RSS Df Sum
of Sq F Pr(>F)
1
521 4606.6
2
520 4604.5 1 2.0835 0.2353 0.6278
También podemos utilizar el
estadístico t para testear si beduc + bexper = 1. Rechazamos la hipótesis
nula de que ambos coeficientes sean iguales a 1.
>
# Utilice el estadístico de prueba
>
# h0: beduc + bexper = 1
>
# h0: beduc + bexper no son iguales 1
>
# alpha = 5%
>
tc3<-(beduc+bexper-1)/sqrt(mvc[2,2]+mvc[3,3]+2*mvc[2,3])
>
tc3
educ
-3.309629
> alpha4<-0.1
>
tt4 <- qt(1-alpha4, glb)
>
tt4
[1]
1.283182
> # Regla de rechazo beduc +
bexper == 1
>
paste("Rechazamos H0?",abs(tc3)>abs(tt4))
[1]
"Rechazamos H0? TRUE"
3.2. Contraste de
restricciones de exclusión (test F)
Nuevamente verificamos una
alternativa de estimación. Utilizando un contraste F, de restricciones de exclusión.
>
# CAR ----
>
modeloPUCMM
Call:
lm(formula
= wage ~ educ + exper + expersq + female + services,
data = wage1)
Coefficients:
(Intercept)
educ exper
expersq female
services
-2.176162 0.550638 0.253904
-0.004396 -2.049511 -1.022515
> library(car)
>
linearHypothesis(modeloPUCMM, c("educ=0", "exper=0"))
Linear
hypothesis test
Hypothesis:
educ
= 0
exper
= 0
Model 1: restricted model
Model
2: wage ~ educ + exper + expersq + female + services
Res.Df RSS Df Sum
of Sq F Pr(>F)
1
522 6247.9
2
520 4604.5 2 1643.4 92.797 < 2.2e-16 ***
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
3.3. El estadístico F para
la significatividad conjunta de una regresión
> linearHypothesis(modeloPUCMM,
c("educ=0", "exper=0", "expersq=0",
"female=0", "services=0"))
Linear
hypothesis test
Hypothesis:
educ = 0
exper = 0
expersq = 0
female = 0
services =
0
Model 1:
restricted model
Model 2:
wage ~ educ + exper + expersq + female + services
Res.Df
RSS Df Sum of Sq F Pr(>F)
1 525 7160.4
2 520 4604.5
5 2555.9 57.73 < 2.2e-16 ***
---
Signif.
codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05
‘.’ 0.1 ‘ ’ 1
Verifique que este es el test de significancia global que R nos
brinda de forma automática con el resultado del modelo de regresión.
F-statistic:
57.73 on 5 and 520 DF, p-value: < 2.2e-16