Análisis del Impacto de un Choque Monetario sobre el Desempleo usando VAR en R

 En este post, exploraremos cómo estimar un modelo VAR en R utilizando la base de datos Canada del paquete vars. Se intenta mostrar cómo usar impulso respuesta de un VAR y como generar escenarios a partir de la introducción de choques. Nos enfocaremos en analizar la respuesta del desempleo ante un choque monetario, graficar la función de impulso-respuesta (IRF) y proyectar la tasa de desempleo con y sin la presencia del choque.

Antes de comenzar, asegurémonos de tener instalados y cargados los paquetes necesarios:
 
library(vars)
library(ggplot2)
library(forecast)

Utilizaremos la base Canada, que contiene datos macroeconómicos de Canadá. Seleccionaremos la tasa de desempleo (U) y la tasa de interés (R) para modelar su relación mediante un VAR con dos rezagos.
 
# Cargar la base de datos
data(Canada)
Canada_ts <- as.data.frame(Canada)
 
# Estimar un modelo VAR con 2 rezagos
desempleo_VAR <- VAR(Canada_ts, p = 2, type = "const")
 
Funciones de Impulso-Respuesta (IRF)

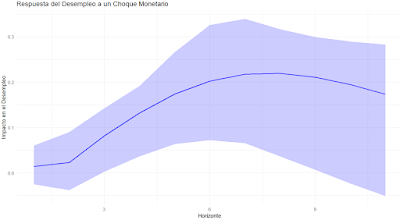
Ahora obtenemos la función de impulso-respuesta para analizar el efecto de un choque monetario (en la tasa de interés R) sobre el desempleo (U).
 
irf_result <- irf(desempleo_VAR, impulse = "rw", response = "U", n.ahead = 10, boot = TRUE)
 
irf_df <- data.frame(
  Horizon = 1:11,
  Response = irf_result$irf$rw |> as.vector(),
  Lower = irf_result$Lower$rw |> as.vector(),
  Upper = irf_result$Upper$rw |> as.vector()
)
 
ggplot(irf_df, aes(x = Horizon, y = Response)) +
  geom_line(color = "blue", size = 1) +
  geom_ribbon(aes(ymin = Lower, ymax = Upper), fill = "blue", alpha = 0.2) +
  labs(title = "Respuesta del Desempleo a un Choque Monetario",
       x = "Horizonte",
       y = "Impacto en el Desempleo") +
  theme_minimal()
 

Proyección del Desempleo sin Choque
 
Ahora realizamos una proyección de la tasa de desempleo para los próximos 10 períodos sin ningún choque:
 
forecasts <- predict(desempleo_VAR, n.ahead = 10)
U_forecast <- data.frame(
  Horizon = 1:10,
  Forecast = forecasts$fcst$U[, 1]
)

Proyección del Desempleo con un Choque Monetario

En un modelo VAR (Vector Autoregressive), un choque se refiere a una perturbación o innovación inesperada que afecta a una o más variables del sistema. Estos choques representan eventos imprevistos que alteran la trayectoria normal de las variables económicas o financieras modeladas.

Un choque en un modelo VAR tiene las siguientes características:
·        Es una perturbación exógena que entra al sistema a través de los términos de error en las ecuaciones del modelo
·        Puede afectar simultáneamente a múltiples variables debido a la estructura multivariante del VAR
·        Permite analizar la propagación de efectos a lo largo del tiempo (mediante funciones de impulso-respuesta)
·        Ayuda a entender cómo un cambio inesperado en una variable afecta a las demás variables del sistema
 
Introducimos un choque en la tasa de interés (+0.5 puntos porcentuales en el primer período) y ajustamos la predicción:
 
forecasts <- predict(desempleo_VAR, n.ahead = 10)
 
U_forecast <- data.frame(
  Horizon = 1:10,
  Forecast = forecasts$fcst$U[, 1]
)
 
  shock <- rep(0, 10)
shock[1] <- 0.5  # Simulamos un aumento de 0.5 pp en la tasa de interés
response_with_shock <- irf_result$irf$rw[-11] + shock  # Aplicamos el choque a la IRF
 
U_forecast_shock <- data.frame(
  Horizon = 1:10,
  Forecast = U_forecast$Forecast + response_with_shock
)
 
ggplot() +
  geom_line(data = U_forecast, aes(x = Horizon, y = Forecast, color = "Sin Choque"), size = 1) +
  geom_line(data = U_forecast_shock, aes(x = Horizon, y = Forecast, color = "Con Choque"), size = 1) +
  labs(title = "Proyección del Desempleo con y sin Choque Monetario",
       x = "Horizonte",
       y = "Tasa de Desempleo") +
  scale_color_manual(name = "Escenario", values = c("Sin Choque" = "black", "Con Choque" = "red")) +
  theme_minimal()