En
la siguiente entrada se muestra la estimación del Valor en Riesgo (VaR, Value at Risk) para los precios de un
determinado índice financiero, para esto se utiliza el método delta-normal y VaR
condicional combinando la estrategia ARIMA con la GARCH. Se utiliza la data EuStockMarkets disponible en R, tal como se muestra en los siguientes codigos:
library(rugarch)
library(ggfortify)
library(ggplot2)
library(ggthemes)
library(forecast)
library(tseries)
library(gridExtra)
DAX <- EuStockMarkets[,"DAX"]
returnx <-
diff(log(DAX))*100
#
_________________________________________________________
p1 = qplot(x = 1:length(returnx) , y = returnx , geom
= 'line') +
geom_line(color = 'darkblue') +
geom_hline(yintercept = mean(returnx) , color = 'red' , size = 1) +
labs(x = '' ,
y = 'Daily Returns')
p2 = qplot(returnx , geom = 'density') +
coord_flip() +
geom_vline(xintercept = mean(returnx) , color = 'red' , size = 1) +
geom_density(fill = 'lightblue' , alpha = 0.4) + labs(x = '')
grid.arrange(p1 , p2 , ncol = 2)
Ya
el gráfico de las rentabilidades apunta a que la serie estudiada muestra
volatilidades cambiantes en el tiempo y que tiende agruparse alrededor de
episodios de distintos niveles de incertidumbre en las series, características
frecuentes en series financieras de alta frecuencia. Sin embargo, un estudio
formal de la heterocedasticidad en las series se obtiene a partir de un test
ARCH o de autocorrelación del cuadrado de las rentabilidades. El comando Box.test aplica el test de
Box-Pierce sobre la serie de rentabilidades:
Box.test(returnx**2, lag = 1, type =
"Ljung")
Box-Ljung
test
data: returnx^2
X-squared = 11.596, df = 1, p-value = 0.0006609
Estimación del modelo ARMA-GARCH
Según
los resultados se rechaza la hipótesis nula de no autocorrelación en el
cuadrado del retorno, lo que se asume como evidencia de heterocedasticidad. Posterior
al estudio de la heterocedasticidad en la varianza, realizamos la
especificación del modelo ARMA-GARCH asumiendo una distribución normal. Para
entender la estimación de este modelo piense en la función de verosimilitud de
una normal, donde la media y la varianza cambian en el tiempo, siguiendo el modelo
ARIMA y GARCH, respectivamente.
En
los códigos siguientes usamos la función ugarchspec para especificar el
modelo GARCH(1,1) como modelo de varianza (variance.model) indicándole el tipo de
GARCH a estimar ("sGARCH") y el orden del mismo (c(1,
1)),
que corresponden al beta y alpha respectivamente.
Adicionalmente, se indica el orden del modelo ARMA (c(1,1)) que corresponde al
proceso auto regresivo y de media móvil respectivamente (note que el proceso
ARMA no comprende un orden de integración de las series, por ende, debe
asegurarse que la serie usada es un proceso estacionario o I(0)). Finalmente se
presenta la distribución asumida (distribution.model). Respecto a este
último punto, debe tener pendiente que se asume una distribución normal de los
datos, siendo en algunos casos necesario asumir otros tipos de distribuciones
que se ajusten mejor a nuestros datos. Finalmente, la estimación del modelo se
realiza mediante el comando ugarchfit.
## Especificación del modelo
spec <- ugarchspec(variance.model = list(model = "sGARCH",
garchOrder = c(1, 1)),
mean.model =
list(armaOrder = c(1,1)),
distribution.model = "normal")
fit_mod <- ugarchfit(spec, data = returnx)
La
función sigma permite recuperar la volatilidad histórica de la serie, este
proceso solo se realiza una vez se ha validado el modelo estimado. Esto es, los
residuos estandarizados se comportan como un ruido blanco.
vol_hist <- sigma(fit_mod)
plot(vol_hist)
Antes
de poder usar el modelo, debemos obtener los residuos estandarizados para
validarlo. Esta validación, tal como el resto de los modelos de serie
temporales, requieren que el residuo se comparte como de manera aleatoria. En
el siguiente ejemplo se utiliza el test de Box-Pierce, cuya hipótesis nula es
que la serie no tiene autocorrelación, sobre los residuos estandarizados, para
validar el modelo usado. Por tanto, usando el p-valor del test, claramente no
rechazamos h0.
rs <- residuals(fit_mod, standardize = TRUE)
Box.test(rs, lag = 1, type = "Ljung")
Box-Ljung
test
data: rs
X-squared = 1.963, df = 1, p-value = 0.1612
VaR
incondicional: enfoque Delta-Normal
VaR(c)= -mean(R) -
sqrt(sigma)*qnorm(c)
VaRincon <- mean(returnx) + sd(returnx) *
qnorm(0.01)
VaRincon
[1] -2.331129
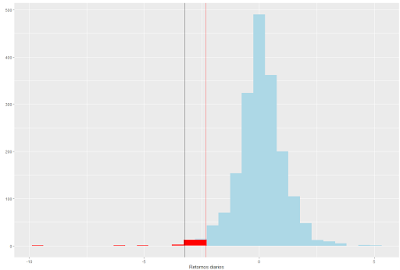
qplot(returnx , geom = 'histogram') +
geom_histogram(fill = 'lightblue' , bins = 30) +
geom_histogram(aes(returnx[returnx < VaRincon]) , fill = 'red' , bins
= 30) +
geom_vline(aes(xintercept = VaRincon),
colour="red") +
labs(x = 'Retornos diarios')
esVaR <- mean(returnx[returnx < VaRincon])
esVaR
[1] -2.331129
qplot(returnx , geom = 'histogram') +
geom_histogram(fill = 'lightblue' , bins = 30) +
geom_histogram(aes(returnx[returnx < VaRincon]) , fill = 'red' , bins
= 30) +
geom_vline(aes(xintercept = VaRincon),
colour="red") +
geom_vline(aes(xintercept = esVaR),
colour="black") +
labs(x = 'Retornos diarios')
Ahora,
dado que identificamos la ausencia de autocorrelación en los residuos y los
residuos al cuadrado, podemos usar la serie histórica de volatilidades para
obtener el VaR condicional.
#VaR condicional
alpha <- 0.99
VaR_hist <- quantile(fit_mod, probs = alpha)
autoplot(VaR_hist, ts.colour = 'firebrick1')
fit_mod@fit$coef
mu ar1 ma1 omega alpha1 beta1 shape
0.07714178
0.67596085 -0.70016405
0.02079888 0.07720194 0.90635090
5.89322679
nu
<- fit_mod@fit$coef[["shape"]]
VaR_hist1 <- fitted(fit_mod) + vol_hist *
sqrt((nu-2)/nu) * qt(alpha, df = nu)
#VaR Plot
plot(-as.vector(VaR_hist1), type = "l", col
= 4)
abline(h=VaRincon, col = 2)
legend('bottomleft', c("VaR GARCH",
"VaR incondicional") ,
lty=1,
col=c(4,2), bty='n', cex=.75)
Backtesting
Finalmente,
necesitamos validar que tan bien el modelo VaR replica las condiciones
históricas de mi serie. Para esto, se verifican que la cantidad de veces en que
las rentabilidades observadas superen el límite establecido por el VaR
condicional.
n<-length(returnx)
btest <- VaRTest(1-alpha,
actual = -returnx,
VaR = quantile(ugarchfit(spec, data = -returnx), probs = 1-alpha))
El
número de excepciones está en función del nivel de significancia = (1-alpha) *
n:
(1-alpha)
* n
[1]
18.59
El
total de excepciones se contabilizan con;
btest$actual.exceed
[1] 10
Data = data.frame(returnx, -VaR_hist,
fecha=time(EuStockMarkets[-1,]))
ggplot(Data) +
geom_line(aes(x = fecha, y =
returnx), color = "gray") +
geom_line(aes(x = fecha, y =
q.0.99.), color = "blue") +
geom_point(data=Data[Data$returnx<Data$q.0.99.,], aes(x=fecha,
y=q.0.99.), colour="red", size=5)
Referencias
Angelidis T., Benos A. and Degiannakis S. (2003). The
Use of GARCH Models in VaR Estimation.
Hofert, Marius (2019). Fitting and Predicting VaR
based on an ARMA-GARCH Process.
Proietti, Giorgio (2018). ARCH & GARCH models,
application on R with rugarch package.
Prvulovic, Dejan (2017). VaR with GARCH(1,1).
Rpubs.com.
Robinzonov, Nikolay (2013). Risk Management Using R.